Cho hàm số
. Đồ thị hàm số
như hình bên. Hỏi hàm số
nghịch biến trên khoảng nào trong các khoảng sau?
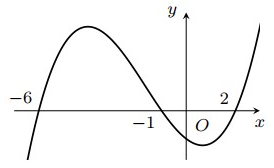
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: D
Cho hàm số
. Đồ thị hàm số
như hình bên. Hỏi hàm số
nghịch biến trên khoảng nào trong các khoảng sau?

.
.
.
.
Đáp án đúng là: D
Cho hàm số
. Đồ thị hàm số
như hình bên. Hỏi hàm số
nghịch biến trên khoảng nào trong các khoảng sau?
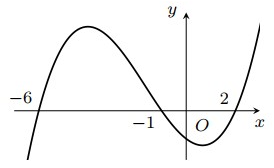
A. . B. . C. . D. .
Lời giải
Ta có .
Phương trình
Lập bảng xét dấu đạo hàm của hàm số

Dựa vào bảng xét dấu đạo hàm, ta thấy hàm số nghịch biến trên khoảng .
Câu hỏi tương tự:
#7513 THPT Quốc giaToán
Cho hàm số
. Đồ thị hàm số
như hình vẽ bên dưới và
.
Hàm số đồng biến trên khoảng nào trong các khoảng sau?
Lượt xem: 127,871 Cập nhật lúc: 03:20 08/04/2025
#7599 THPT Quốc giaToán
Cho hàm số
có đồ thị hàm số
như hình vẽ bên
Hàm số đồng biến trên khoảng nào dưới đây?
Lượt xem: 129,275 Cập nhật lúc: 09:55 07/04/2025
#7563 THPT Quốc giaToán
Cho hàm số
có
và đồ thị của hàm số
như hình bên dưới
Hỏi hàm số , ( là tham số) có nhiều nhất bao nhiêu điểm cực trị trên nửa khoảng
Lượt xem: 128,714 Cập nhật lúc: 21:12 06/04/2025
#8864 THPT Quốc giaToán
Cho hàm số
có
và đồ thị của hàm số
như hình bên dưới.
Hỏi hàm số , ( là tham số) có nhiều nhất bao nhiêu điểm cực trị trên nửa khoảng ?
Lượt xem: 150,825 Cập nhật lúc: 01:05 08/04/2025
#8251 THPT Quốc giaToán
Cho hàm số
có đạo hàm trên
, đồ thị hàm số
như trong hình vẽ bên.
Hỏi phương trình có tất cả bao nhiêu nghiệm biết ?
Lượt xem: 140,402 Cập nhật lúc: 03:49 07/04/2025
#8128 THPT Quốc giaToán
Cho đồ thị hàm số
như hình bên. Khẳng định nào sau đây sai?
Lượt xem: 138,410 Cập nhật lúc: 12:52 07/04/2025
#8942 THPT Quốc giaToán
Cho hàm số
xác định trên
và có bảng biến thiên như hình vẽ bên. Đồ thị hàm số
cắt trục hoành tại bao nhiêu điểm?
Lượt xem: 152,089 Cập nhật lúc: 01:12 07/04/2025
#8447 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ bên. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho bằng
Lượt xem: 143,753 Cập nhật lúc: 04:10 07/04/2025
#8590 THPT Quốc giaToán
Cho hai hàm đa thức
liên tục trên
, có đồ thị là hai đường cong như hình bên dưới. Biết rằng đồ thị hàm số
có đúng một cực trị là
, đồ thị hàm số
có đúng một điểm cực trị là
và
. Số giá trị nguyên của tham số
để hàm số
có đúng
điểm cực trị là.
Lượt xem: 146,114 Cập nhật lúc: 14:26 06/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 50 phút
48720
