Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7870

Cho hàm số y = x^{6} + \left(\right. m + 4 \right) x^{5} + \left( 16 - m^{2} \right) x^{4} + 2. Gọi SS là tập hợp các giá trị nguyên dương của tham số mm để hàm số đã cho đạt cực tiểu tại x=0x = 0. Tổng các phần tử của SS bằng

A.  

9.

B.  

6.

C.  

8.

D.  

3.

Đáp án đúng là: B

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình thang vuông tại AA và BB, AB=BC=aA B = B C = a, AD=2a.A D = 2 a . Tam giác SADS A D đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Diện tích mặt cầu ngoại tiếp hình chóp S.ABCS . A B C là
A. 6πa26 \pi a^{2}. B. 10πa210 \pi a^{2}. C. 5πa25 \pi a^{2}. D. 3πa23 \pi a^{2}.
Lời giải
Chọn C



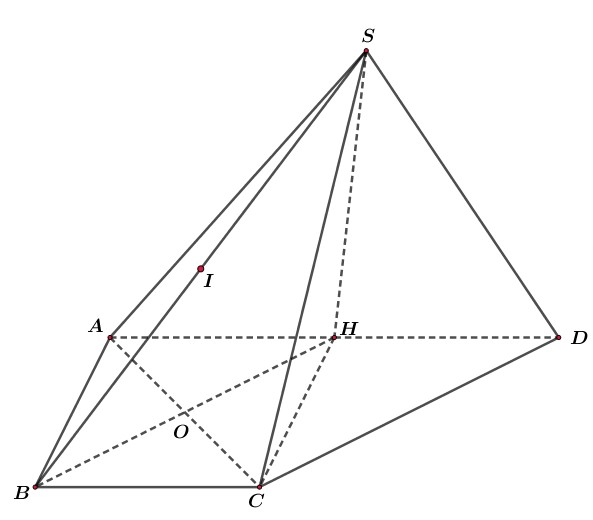
Gọi HHlà trung điểm của ADA D ⇒SH⊥AD\Rightarrow S H \bot A D ( do tam giác SADS A D đều).
Ta có
Gọi O=AC∩BHO = A C \cap B H, II là trung điểm của SBS B ⇒OI\Rightarrow O I là trục của đường tròn ngoại tiếp tam giác ABCA B C II ⇒IA=IB=IC\Rightarrow I A = I B = I C(1)
Mà IB=ISI B = I S(2)
Từ (1) và (2) suy ra II là tâm mặt cầu ngoại tiếp hình chóp S.ABCS . A B C.
⇒R=SB2=SH2+BH22=(a3)2+(a2)22=a52\Rightarrow R = \dfrac{S B}{2} = \dfrac{\sqrt{S H^{2} + B H^{2}}}{2} = \dfrac{\sqrt{\left( a \sqrt{3} \right)^{2} + \left( a \sqrt{2} \right)^{2}}}{2} = \dfrac{a \sqrt{5}}{2}
⇒\Rightarrow diện tích mặt cầu ngoại tiếp hình chóp S.ABCS . A B C là 4πR2=5πa24 \pi R^{2} = 5 \pi a^{2}.


 

Câu hỏi tương tự:

#8900 THPT Quốc giaToán

Cho hàm số y=x3−3(m+1)x2+9x−my = x^{3} - 3 \left( m + 1 \right) x^{2} + 9 x - m với mm là tham số. Gọi SS là tập hợp các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x1,x2x_{1} , x_{2} sao cho 3x1−2x2=m+63 x_{1} - 2 x_{2} = m + 6. Tích các phần tử của tập SS bằng

Lượt xem: 151,394 Cập nhật lúc: 13:03 18/01/2025

#8098 THPT Quốc giaToán

Cho hàm số y=2x3−3(m+1)x2+6mx−2y = 2 x^{3} - 3 \left( m + 1 \right) x^{2} + 6 m x - 2. Gọi SS là tập hợp tất cả các giá trị
nguyên của tham số mm để hàm số có hai cực trị cùng dấu. Số phần tử của SS là

Lượt xem: 137,700 Cập nhật lúc: 09:25 17/01/2025

#7602 THPT Quốc giaToán

Cho hàm số f(x)=x2−2x+1f \left( x \right) = x^{2} - 2 x + 1. Gọi SS là tập hợp tất cả các giá trị thực của tham số mm để giá trị lớn nhất của hàm số g(x)=∣f2(x)−2f(x)+m∣g \left( x \right) = \left|\right. f^{2} \left( x \right) - 2 f \left( x \right) + m \left|\right. trên đoạn [−1;3]\left[\right. - 1 ; 3 \left]\right. bằng 88. Tính tổng các phần tử của SS.

Lượt xem: 129,276 Cập nhật lúc: 05:27 07/01/2025

#8091 THPT Quốc giaToán

Cho hàm số y=x3+mx2+(2m2−m+1)x+m2−3m.y = x^{3} + m x^{2} + \left( 2 m^{2} - m + 1 \right) x + m^{2} - 3 m . Gọi SS là tập hợp tất cả các giá trị thực của tham số mm sao cho giá trị lớn nhất của hàm số trên (−∞;  0]\left(\right. - \infty ; \textrm{ }\textrm{ } 0 \left]\right. bằng −2.- 2 . Tích các phần tử của SS bằng

Lượt xem: 137,584 Cập nhật lúc: 02:01 17/01/2025

#8505 THPT Quốc giaToán

Cho hàm số y=mx−2m−3x−my = \dfrac{m x - 2 m - 3}{x - m} với mm là tham số. Gọi SS là tập hợp tất cả các giá trị nguyên của mm để hàm số đồng biến trên khoảng (2;+∞)\left( 2 ; + \infty \right). Tìm số phần tử của SS

Lượt xem: 144,696 Cập nhật lúc: 13:22 18/01/2025

#8338 THPT Quốc giaToán

Cho hàm số y=2xx+1y = \dfrac{2 x}{x + 1} có đồ thị (C)\left( C \right) và điểm A(0; a)A \left( 0 ; \textrm{ } a \right). Gọi SS là tập hợp tất cả các giá trị thực của aa để từ AA kẻ được hai tiếp tuyến AM, ANA M , \textrm{ } A N đến (C)\left( C \right) với M, NM , \textrm{ } N là các tiếp điểm và MN=4.M N = 4 . Tổng tất cả các phần tử của SS bằng

Lượt xem: 141,853 Cập nhật lúc: 18:29 18/01/2025

#7885 THPT Quốc giaToán

Gọi SS là tập hợp tất cả các giá trị nguyên của tham số sao cho hàm số

xác định với mọi x∈(1;+∞).x \in \left( 1 ; + \infty \right) .Tổng tất cả các phần tử của tập SS bằng

Lượt xem: 134,143 Cập nhật lúc: 03:40 17/01/2025

#8535 THPT Quốc giaToán

Xét hàm số f(t)=9t9t+m2f \left( t \right) = \dfrac{9^{t}}{9^{t} + m^{2}} với mm là tham số thực. Gọi SS là tập hợp tất cả các giá trị của mm sao cho Tìm tổng các phần tử của tập SS.

Lượt xem: 145,191 Cập nhật lúc: 18:24 18/01/2025

#8337 THPT Quốc giaToán

Cho hàm số f(x)=x2−2xf \left( x \right) = x^{2} - 2 x. Gọi SS là tập các giá trị mm để giá trị lớn nhất của hàm số g(x)=∣f(1+sinx)+m∣g \left( x \right) = \left| f \left(\right. 1 + sin x \right) + m \left|\right. bằng 3. Tích các phần tử của S bằng

Lượt xem: 141,826 Cập nhật lúc: 17:37 17/01/2025


Đề thi chứa câu hỏi này:

24. Đề thi thử TN THPT môn Toán năm 2024 - THPT CHUYÊN LAM SƠN - THANH HÓA - LẦN 1THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,935 lượt xem 2,618 lượt làm bài