Giá trị lớn nhất của hàm số
trên khoảng
bằng:
A. 1 .
B. 3.
C. -1 .
D. 5 .
Đáp án đúng là: B
Giá trị lớn nhất của hàm số trên khoảng bằng:
1 .
3.
-1 .
5 .
Đáp án đúng là: B
(TH):
Phương pháp:
Khảo sát, lập BBT của hàm số trên
và xác định GTLN của hàm số.
Cách giải:
Hàm số
có:
.
Giải
BBT:
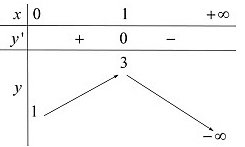
Vậy .
Câu hỏi tương tự:
#7552 THPT Quốc giaToán
Tìm để giá trị lớn nhất của hàm số trên đoạn là nhỏ nhất. Giá trị của thuộc khoảng nào?
Lượt xem: 128,481 Cập nhật lúc: 19:50 25/04/2025
#8339 THPT Quốc giaToán
Giá trị lớn nhất của hàm số trên bằng 3. Giá trị nhỏ nhất của hàm số trên đoạn bằng bao nhiêu?
Lượt xem: 141,855 Cập nhật lúc: 21:54 24/04/2025
#7723 THPT Quốc giaToán
Giá trị lớn nhất của hàm số trên đoạn bằng
Lượt xem: 131,378 Cập nhật lúc: 19:15 25/04/2025
#8999 THPT Quốc giaToán
Giá trị lớn nhất của hàm số trên là
Lượt xem: 153,522 Cập nhật lúc: 17:11 25/04/2025
#7875 THPT Quốc giaToán
Biết giá trị lớn nhất của hàm số trên đoạn bằng 3. Giá trị của tham số m là
Lượt xem: 133,966 Cập nhật lúc: 02:54 23/04/2025
#7759 THPT Quốc giaToán
Tìm giá trị lớn nhất của hàm số trên đoạn
Lượt xem: 132,008 Cập nhật lúc: 01:48 26/04/2025
#7553 THPT Quốc giaToán
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn là
Lượt xem: 128,517 Cập nhật lúc: 22:59 25/04/2025
#8399 THPT Quốc giaToán
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn :
Lượt xem: 142,891 Cập nhật lúc: 17:46 24/04/2025
#8165 THPT Quốc giaToán
Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn Khi đó tích và bằng
Lượt xem: 138,938 Cập nhật lúc: 16:25 25/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
5,138 xem384 thi
