Số giá trị nguyên âm của tham số $m$ để phương trình $\left(\text{e}\right)^{x} + m = \dfrac{4}{5^{x} - 1} + \dfrac{2}{5^{x} - 2}$ có hai nghiệm phân biệt là

A.  

$4$.

B.  

$3$.

C.  

$5$.

D.  

$6$.

Đáp án đúng là: C

Số giá trị nguyên âm của tham số $m$ để phương trình $\left(\text{e}\right)^{x} + m = \dfrac{4}{5^{x} - 1} + \dfrac{2}{5^{x} - 2}$ có hai nghiệm phân biệt là
A. $4$. B. $3$. C. $5$. D. $6$.
Lời giải
Phương trình $\left(\text{e}\right)^{x} + m = \dfrac{4}{5^{x} - 1} + \dfrac{2}{5^{x} - 2} \Leftrightarrow m = \dfrac{4}{5^{x} - 1} + \dfrac{2}{5^{x} - 2} - \left(\text{e}\right)^{x}$.
Đặt $f \left( x \right) = \dfrac{4}{5^{x} - 1} + \dfrac{2}{5^{x} - 2} - \left(\text{e}\right)^{x}$. Tập xác định $D = \mathbb{R} \left{ 0 ; \left(log\right)_{5} 2 \right}$.
$f^{'} \left( x \right) = - 4 . \dfrac{5^{x} ln5}{\left(\left( 5^{x} - 1 \right)\right)^{2}} - 2 . \dfrac{5^{x} ln5}{\left(\left( 5^{x} - 2 \right)\right)^{2}} - \left(\text{e}\right)^{x} < 0 , \textrm{ } \forall x \in D$.
Lập bảng biến thiên

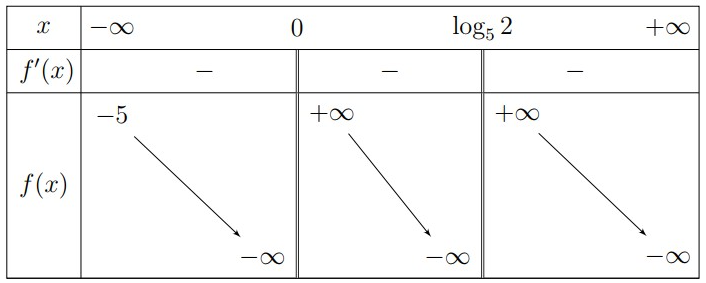
Dựa vào bảng biến thiên, ta thấy phương trình có hai nghiệm phân biệt khi và chỉ khi $m \geq - 5$.
Vậy có $5$ giá trị nguyên âm của tham số $m$ để phương trình $\left(\text{e}\right)^{x} + m = \dfrac{4}{5^{x} - 1} + \dfrac{2}{5^{x} - 2}$ có hai nghiệm phân biệt.