Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8190

Số giá trị nguyên của tham số m để hàm số y = m x^{4} - \left(\right. m - 3 \right) x^{2} + m^{2} không có điểm cực đại là

A.  

4.

B.  

2.

C.  

0.

D.  

vô số.

Đáp án đúng là: A

Số giá trị nguyên của tham số m để hàm số y=mx4−(m−3)x2+m2y = m x^{4} - \left( m - 3 \right) x^{2} + m^{2} không có điểm cực đại là
A. 4. B. 2. C. 0. D. vô số.
Lời giải
• Nếu m=0m = 0 thì y=3x2y = 3 x^{2}. Hàm số chỉ có điểm cực tiểu x = 0. Do đó m=0m = 0 thỏa mãn.
• Nếu m≠0m \neq 0 thì hàm số đã cho là hàm bậc bốn trùng phương.
✓ Nếu m(3−m)<0m \left( 3 - m \right) < 0 thì hàm số có 3 điểm cực trị. Khi đó hàm số có điểm cực đại (không
thỏa mãn yêu cầu đề bài).
✓ Nếu m(3−m)≥0⇔0<m≤3m \left( 3 - m \right) \geq 0 \Leftrightarrow 0 < m \leq 3 thì hàm số có 1 điểm cực trị và đồ thị hàm số có dạng như
hình vẽ dưới đây



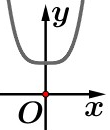
Khi đó hàm số không có điểm cực đại (thỏa mãn yêu cầu đề bài).
Vậy có 4 giá trị nguyên m thỏa mãn là 0; 1; 2; 3.


 

Câu hỏi tương tự:

#8386 THPT Quốc giaToán

Có tất cả bao nhiêu giả trị nguyên của tham số m để hàm số luôn đồng biển trên khoảng ?

Lượt xem: 142,630 Cập nhật lúc: 14:08 23/11/2024

#8897 THPT Quốc giaToán

Có bao nhiêu giá trị nguyên của tham số m để phương trình (16)(log)3∣cosx∣+(12)(log)3(cos)2x−(cos)2x=2−m2+6m\left(16\right)^{\left(log\right)_{3} \left|\right. cos x \left|\right.} + \left(12\right)^{\left(log\right)_{3} \left(cos\right)^{2} x} - \left(cos\right)^{2} x = 2^{- m^{2} + 6 m} vô nghiệm?

Lượt xem: 151,288 Cập nhật lúc: 05:14 23/11/2024

#7919 THPT Quốc giaToán

Cho phương trình (m là tham số thực ). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm ?

Lượt xem: 134,696 Cập nhật lúc: 10:10 23/11/2024

#7520 THPT Quốc giaToán

Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn sao cho đồ thị hàm số y=x−1x2−2mx+3m+10y = \dfrac{x - 1}{x^{2} - 2 m x + 3 m + 10} có đúng 2 đường tiệm cận đứng.

Lượt xem: 127,908 Cập nhật lúc: 01:34 24/11/2024

#8926 THPT Quốc giaToán

Số giá trị nguyên của tham số mm để hàm số đồng biến trên khoảng là

Lượt xem: 151,805 Cập nhật lúc: 06:05 24/11/2024

#7677 THPT Quốc giaToán

Cho hàm số bậc ba f(x)f \left( x \right) có đồ thị như hình vẽ. Số giá trị nguyên của tham số mm đề phương trình f(x)+1=mf \left( x \right) + 1 = m có 33 nghiệm phân biệt là


Lượt xem: 130,559 Cập nhật lúc: 17:00 22/11/2024

#8688 THPT Quốc giaToán

Cho hàm số bậc ba y=f(x)y = f \left( x \right) có đồ thị là đường cong trong hình vẽ. Số giá trị nguyên của tham số mm để phương trình 3f(x)−m+1=03 f \left( x \right) - m + 1 = 0 có 3 nghiệm phân biệt là


Lượt xem: 147,754 Cập nhật lúc: 01:01 24/11/2024

#8590 THPT Quốc giaToán

Cho hai hàm đa thức y=f(x),y=g(x)y = f \left( x \right) , y = g \left( x \right) liên tục trên R\mathbb{R}, có đồ thị là hai đường cong như hình bên dưới. Biết rằng đồ thị hàm số y=f(x)y = f \left( x \right)có đúng một cực trị là AA, đồ thị hàm số y=g(x)y = g \left( x \right) có đúng một điểm cực trị là BB và AB=10A B = 10. Số giá trị nguyên của tham số mmđể hàm số y=∣∣f(x)−g(x)∣−2m3−4∣y = \left|\right. \left|\right. f \left( x \right) - g \left( x \right) \left|\right. - \dfrac{2 m}{3} - 4 \left|\right. có đúng 77điểm cực trị là.


Lượt xem: 146,068 Cập nhật lúc: 00:14 24/11/2024

#7651 THPT Quốc giaToán

Số giá trị nguyên âm của tham số mm để phương trình (e)x+m=45x−1+25x−2\left(\text{e}\right)^{x} + m = \dfrac{4}{5^{x} - 1} + \dfrac{2}{5^{x} - 2} có hai nghiệm phân biệt là

Lượt xem: 130,117 Cập nhật lúc: 04:08 24/11/2024


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN -SGD-ĐẮK-NÔNG (Bản word kèm giải)THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

1,297 lượt xem 658 lượt làm bài