Có tất cả bao nhiêu giả trị nguyên của tham số m để hàm số y = \left| x^{3} - m x^{2} + 12 x + 2 m \left|\right. luôn đồng biển trên khoảng \left(\right. 1 ; + \infty \right)?

A.  

19.

B.  

18.

C.  

20.

D.  

21.

Đáp án đúng là: C

Có bao nhiêu giá trị nguyên của tham số $m \in \left[ - 10 ; 10 \left]\right.$ để phương trình $\left(16\right)^{x} - 2 \left(\right. m + 1 \right) 4^{x} + 3 m - 8 = 0$ có hai nghiệm trái dấu?
A. 13. B. 7. C. 12. D. 6.
Lời giải
Chọn B
Đặt $t = 4^{x}$, $t > 0$.
Để phương trình $\left(16\right)^{x} - 2 \left( m + 1 \right) 4^{x} + 3 m - 8 = 0$ có hai nghiệm trái dấu thì phương trình $t^{2} - 2 \left( m + 1 \right) t + 3 m - 8 = 0$ có hai nghiệm $0 < t_{1} < 1 < t_{2}$.
Ta có $t^{2} - 2 \left( m + 1 \right) t + 3 m - 8 = 0 \Leftrightarrow t^{2} - 2 t - 8 = \left( 2 t - 3 \right) m \text{ }(\text{1})$.
Ta có $t = \dfrac{3}{2}$ không là nghiệm của (1)
Với $t \neq \dfrac{3}{2}$ Khi đó phương trình $\left( 1 \right) \Leftrightarrow m = \dfrac{t^{2} - 2 t - 8}{2 t - 3}$
Xét hàm số $g \left( t \right) = \dfrac{t^{2} - 2 t - 8}{2 t - 3}$.
Ta có $g^{'} \left( t \right) = \dfrac{2 t^{2} - 6 t + 22}{\left( 2 t - 3 \right)^{2}} > 0 , t \neq \dfrac{3}{2}$.
Bảng biến thiên:

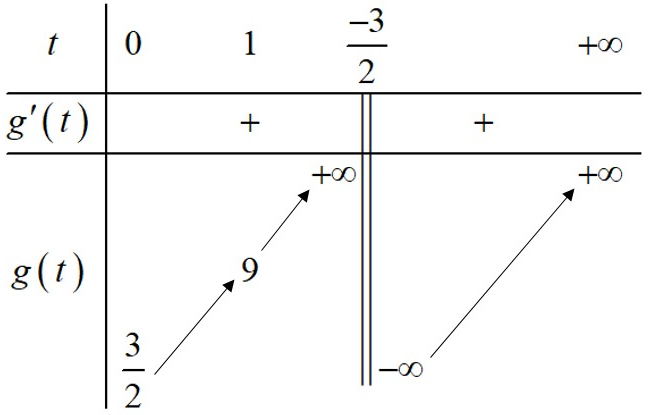
Từ bảng biến thiên, để phương trình $t^{2} - 2 \left( m + 1 \right) t + 3 m - 8 = 0$ có hai nghiệm $0 < t_{1} < 1 < t_{2}$ khi và chỉ khi $\dfrac{3}{2} < m < 9$ $\Rightarrow m \in \left{ 2 ; 3 ; . . . ; 8 \right}$.