Trong không gian Oxyz, cho mặt cầu  $\left( S \right) : \textrm{ } \left( x - 1 \right)^{2} + \left( y - 2 \right)^{2} + \left( z - 3 \right)^{2} = 1$ và điểm  $A \left( 2 ; 3 ; 4 \right)$. Xét các điểm  $M$ thuộc  $\left( S \right)$ sao cho  $A M$ luôn tiếp xúc với  $\left( S \right)$,  $M$ luôn thuộc mặt phẳng có phương trình là

A.  

$x + y + z + 7 = 0$.

B.  

$x + y + z - 7 = 0$.

C.  

$2 x + 2 y + 2 z - 15 = 0$.

D.  

$2 x + 2 y + 2 z + 15 = 0 .$

Đáp án đúng là: B

Ta có mặt cầu  $\left( S \right) : \textrm{ } \left( x - 1 \right)^{2} + \left( y - 2 \right)^{2} + \left( z - 3 \right)^{2} = 1$ có tâm  $I \left( 1 ; 2 ; 3 \right) , \textrm{ } R = 1$
Suy ra  $\overset{\rightarrow}{I A} = \left( 1 ; 1 ; 1 \right)$,  $\left|\right. \overset{\rightarrow}{I A} \left|\right. = \sqrt{3} > R$. Vậy điểm  $A$ nằm ngoài mặt cầu  $\left( S \right)$
 

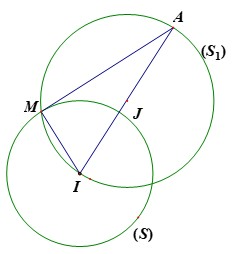
Vì  $AM \bot IM$ nên tập hợp các điểm  $M$ thuộc mặt cầu đường kính  $AI$ có phương trình là  $\left( S_{1} \right) : \textrm{ } \left( x - \dfrac{3}{2} \right)^{2} + \left( y - \dfrac{5}{2} \right)^{2} + \left( z - \dfrac{7}{2} \right)^{2} = \dfrac{3}{4}$. 
Vậy tập hợp các điểm  $M$ là nghiệm của hệ  $\left\{\begin{matrix} \left( S \right) : \textrm{ } \left( x - 1 \right)^{2} + \left( y - 2 \right)^{2} + \left( z - 3 \right)^{2} = 1 \\ \left( S_{1} \right) : \textrm{ } \left( x - \dfrac{3}{2} \right)^{2} + \left( y - \dfrac{5}{2} \right)^{2} + \left( z - \dfrac{7}{2} \right)^{2} = \dfrac{3}{4} \end{matrix}\right.$  $\Rightarrow x + y + z - 7 = 0$