Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7725

Trong không gian với hệ toạ độ OxyzO x y z, cho mặt phẳng (P):x+y+z=0\left( P \right) : x + y + z = 0và mặt cầu (S)\left( S \right) có tâm I(0;1;2)I \left( 0 ; 1 ; 2 \right) bán kính R=1R = 1. Xét điểm MM thay đổi trên (P)\left( P \right). Khối nón có đỉnh II và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ MM đến (S)\left( S \right). Khi (N)\left( N \right) có thể tích lớn nhất, mặt phẳng chứa đường tròn đáy của (N)\left( N \right) có phương trình là x+ay+bz+c=0x + a y + b z + c = 0. Giá trị của a+b+ca + b + c bằng

A.  

0.

B.  

3.

C.  

−2.

D.  

2.

Đáp án đúng là: A


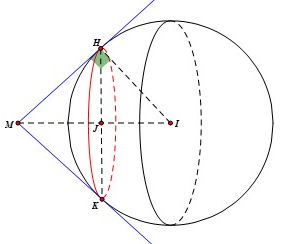
Gọi JJ là tâm đường tròn đáy của (N)\left( N \right) và HH là một điểm trên đường tròn đáy đó.
Ta có (N)\left( N \right) có bán kính đáy r=JHr = J H, đường cao h=JIh = J I; r2+h2=IH2=1⇒r2=1−h2r^{2} + h^{2} = I H^{2} = 1 \Rightarrow r^{2} = 1 - h^{2}.
Thể tích khối nón là
V=13πr2h=13π(1−h2)h=132π(1−h2)(1−h2)2h2V = \dfrac{1}{3} \pi r^{2} h = \dfrac{1}{3} \pi \left( 1 - h^{2} \right) h = \dfrac{1}{3 \sqrt{2}} \pi \sqrt{\left( 1 - h^{2} \right) \left( 1 - h^{2} \right) 2 h^{2}}
≤π32(1−h2+1−h2+2h23)3=23π27\leq \dfrac{\pi}{3 \sqrt{2}} \sqrt{\left( \dfrac{1 - h^{2} + 1 - h^{2} + 2 h^{2}}{3} \right)^{3}} = \dfrac{2 \sqrt{3} \pi}{27}. Dấu "="" = " xảy ra khi h2=13⇔h=33h^{2} = \dfrac{1}{3} \Leftrightarrow h = \dfrac{\sqrt{3}}{3}.
Khi đó IM=IH2IJ=3=d(I,(P))I M = \dfrac{I H^{2}}{I J} = \sqrt{3} = d \left(\right. I , \left( P \right) \left.\right) nên IM⊥(P)I M \bot \left( P \right) hay MM là hình chiếu của II lên (P)\left( P \right).
Ta tìm được M(−1;0;1)M \left( - 1 ; 0 ; 1 \right) và do IJ→=13IM→\overset{\rightarrow}{I J} = \dfrac{1}{3} \overset{\rightarrow}{I M} nên J(−13;23;53)J \left( - \dfrac{1}{3} ; \dfrac{2}{3} ; \dfrac{5}{3} \right).
Suy ra đường tròn đáy của (N)\left( N \right) nằm trên mặt phẳng qua J(−13;23;53)J \left( - \dfrac{1}{3} ; \dfrac{2}{3} ; \dfrac{5}{3} \right) và có véctơ pháp tuyên MI→=(1;1;1)\overset{\rightarrow}{M I} = \left( 1 ; 1 ; 1 \right) nên có phương trình x+y+z−2=0x + y + z - 2 = 0, do đó a=b=1;c=−2a = b = 1 ; c = - 2hay a+b+c=0a + b + c = 0


 

Câu hỏi tương tự:

#8021 THPT Quốc giaToán

Trong không gian với hệ tọa độ  OxyzO x y z cho mặt cầu  (S):x2+y2+z2−2x−2y−2z−1=0\left( \text{S} \right) : x^{2} + y^{2} + z^{2} - 2 x - 2 y - 2 z - 1 = 0và mạt phẳng  (P):x+y+2z+5=0\left( \text{P} \right) : x + y + 2 z + 5 = 0. Lấy điểm  AA di động trên  (S)\left( \text{S} \right)và điểm  BB di động trên (S)\left( \text{S} \right)sao cho  AB→\overset{\rightarrow}{A \text{B}}cùng phương  a→=(−2;1;−1)\overset{\rightarrow}{a} = \left( - 2 ; 1 ; - 1 \right). Tìm giá trị lớn nhất của độ dài đoạn  ABA B.

Lượt xem: 136,457 Cập nhật lúc: 04:05 22/11/2024

#8575 THPT Quốc giaToán

Trong không gian với hệ toạ độ OxyzO x y z, cho mặt phẳng (P):2x+2y−z−3=0\left( P \right) : 2 x + 2 y - z - 3 = 0 và điểm I(1 ; 2 ; −3)I \left( 1 \textrm{ } ; \textrm{ } 2 \textrm{ } ; \textrm{ } - 3 \right). Mặt cầu (S)\left( S \right) tâm II và tiếp xúc (P)\left( P \right) có phương trình:

Lượt xem: 145,869 Cập nhật lúc: 03:08 21/11/2024

#8208 THPT Quốc giaToán

Trong không gian với hệ tọa độ OxyzO x y z, cho mặt phẳng (P):x+y+z+1=0\left( P \right) : x + y + z + 1 = 0 và hai điểm A(1 ; −1 ;2) ,  B(2 ; 1 ;1)A \left( 1 \textrm{ } ; \textrm{ } - 1 \textrm{ } ; 2 \right) \textrm{ } , \textrm{ }\textrm{ } B \left( 2 \textrm{ } ; \textrm{ } 1 \textrm{ } ; 1 \right). Mặt phẳng (Q):ax+by+z+c=0\left( Q \right) : a x + b y + z + c = 0 chứa A ,  BA \textrm{ } , \textrm{ }\textrm{ } B và vuông góc với mặt phẳng (P)\left( P \right), khi đó biểu thức T=a+b+cT = a + b + c có giá trị bằng

Lượt xem: 139,636 Cập nhật lúc: 04:48 22/11/2024

#8254 THPT Quốc giaToán

Trong không gian với hệ tọa độ O x y z , cho mặt phẳng ( P ) : 2 y − z + 3 = 0 và điểm A ( 2 ; 0 ; 0 ) . Mặt phẳng ( α ) đi qua A , vuông góc với ( P ) , cách gốc tọa độ O một khoảng bằng 4 3 và cắt các tia O y , O z lần lượt tại các điểm B và C khác O . Thể tích khối tứ diện O A B C bằng

Lượt xem: 140,389 Cập nhật lúc: 04:16 22/11/2024

#8736 THPT Quốc giaToán

Trong không gian với hệ toạ độ OxyzO x y z, cho điểm M(2;−3;1)M \left( 2 ; - 3 ; 1 \right) và mặt phẳng (α):x+3y−z+2=0\left( \alpha \right) : x + 3 y - z + 2 = 0. Đường thẳng dd đi qua điểm MM và vuông góc với mặt phẳng (α)\left( \alpha \right) có phương trình tham số là:

Lượt xem: 148,617 Cập nhật lúc: 23:15 21/11/2024

#7763 THPT Quốc giaToán

Trong không gian với hệ tọa độ OxyzO x y z, cho đường thẳng (d): x1=y+22=z−1\left( d \right) : \textrm{ } \dfrac{x}{1} = \dfrac{y + 2}{2} = \dfrac{z}{- 1} và mặt phẳng (P):  2x+y+z−1=0\left( P \right) : \textrm{ }\textrm{ } 2 x + y + z - 1 = 0. Phương trình đường thẳng Δ\Delta nằm trong (P)\left( P \right), cắt (d)\left( d \right) và tạo với (d)\left( d \right) một góc 30∘30 \circ đi qua điểm nào sau đây:

Lượt xem: 132,041 Cập nhật lúc: 05:43 22/11/2024

#7662 THPT Quốc giaToán

Trong không gian với hệ tọa độ OxyzO x y z, cho đường thẳng Δ:x−21=y+22=z−2\Delta : \dfrac{x - 2}{1} = \dfrac{y + 2}{2} = \dfrac{z}{- 2} và mặt phẳng (P):2x−y+2z−2022=0\left( P \right) : 2 x - y + 2 z - 2022 = 0. Gọi α\alpha là góc giữa đường thẳng Δ\Delta và mặt phẳng (P)\left( P \right). Khẳng định nào sau đây đúng?

Lượt xem: 130,290 Cập nhật lúc: 06:28 22/11/2024

#7750 THPT Quốc giaToán

Trong không gian với hệ trục tọa độ OxyzO x y z, cho đường thẳng dd và mặt phẳng lần lượt có phương trình x+12=y1=z−21\dfrac{x + 1}{2} = \dfrac{y}{1} = \dfrac{z - 2}{1} và x+y−2z+8=0x + y - 2 z + 8 = 0, điểm A(2;−1;3)A \left( 2 ; - 1 ; 3 \right). Đường thẳng Δ\Delta cắt dd và (P)\left( P \right) lần lượt tại MM và NN sao cho AA là trung điểm của đoạn thẳng MNM N đi qua điểm B(2;m;n)B \left( 2 ; m ; n \right). Tổng m+2nm + 2 n bằng

Lượt xem: 131,780 Cập nhật lúc: 05:17 19/11/2024

#8605 THPT Quốc giaToán

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S)\left( S \right) có tâm thuộc mặt phẳng (P):x+2y+z−7=0\left( P \right) : x + 2 y + z - 7 = 0 và đi qua hai điểm A(1;2;1),  B(2;5;3)A \left( 1 ; 2 ; 1 \right) , \textrm{ }\textrm{ } B \left( 2 ; 5 ; 3 \right). Bán kính nhỏ nhất của mặt cầu (S)\left( S \right) bằng:

Lượt xem: 146,381 Cập nhật lúc: 21:47 21/11/2024


Đề thi chứa câu hỏi này:

82. Đề thi thử TN THPT môn Toán năm 2024 - Sở Hưng YênTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,151 lượt xem 2,212 lượt làm bài