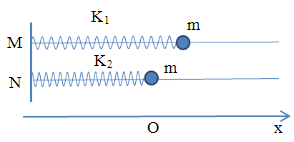
Cho hai con lắc lò xo nằm ngang (k1, m) và (k2, m) như hình vẽ. Trục dao động M và N cách nhau 9cm. Lò xo k1 có độ cứng 100 N/m ; chiều dài tự nhiên l1 = 35cm­. Lò xo k2 ­ ­có độ cứng 25N/m, chiều dài tự nhiên l2 = 26cm. Hai vật có khối lượng cùng bằng m. Thời điểm ban đầu (t = 0), giữ lò xo k1 dãn một đoạn 3cm, lò xo k2 nén một đoạn 6cm rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Bỏ qua mọi ma sát. Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động xấp xỉ bằng :

Cho ba con lắc lò xo dao động điều hòa theo phương nằm ngang. Biết ba lò xo giống hệt nhau và vật nặng có khối lượng tương ứng $m_1,m_2,m_3$. Lần lượt kéo ba vật sao cho ba lò xo giãn cùng một đoạn như nhau rồi thả nhẹ cho ba vật dao động điều hòa. Khi đi qua vị trí cân bằng vận tốc của hai vật $m_1,m_2$ có độ lớn lần lượt là $v_1=20cm/s,v_2=10cm/s$. Biết $m_3=9m_1+4m_2$, độ lớn vận tốc cực đại của vật $m_3$ bằng

Một con lắc lò xo gồm lò xo có chiều dài tự nhiên ${\mathcal{l}}_0=30\mathrm{c}\mathrm{m}$. Kích thích cho con lắc dao động điều hòa theo phương nằm ngang thì chiều dài cực đại của lò xo là $38\mathrm{c}\mathrm{m}$. Khoảng cách ngắn nhất giữa hai thời điểm động năng bằng $n$ lần thế năng và thế năng bằng $n$ lần động năng là $4\mathrm{c}\mathrm{m}$. Giá trị lớn nhất của $n$ gần với giá trị nào nhất sau đây?

Hai con lắc lò xo giống hệt nhau được treo vào hai điểm ở cùng độ cao, cách nhau $3\mathrm{c}\mathrm{m}$. Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng với phương trình lần lượt $x_1=3\mathrm{c}\mathrm{o}\mathrm{s}\omega t$ và $x_2=6\mathrm{c}\mathrm{o}\mathrm{s}(\omega t+\pi /3)\left(\mathrm{c}\mathrm{m}\right)$. Trong quá trình dao động, khoảng cách lớn nhất giữa hai vật nhỏ của các con lắc bằng

Hai con lắc lò xo giống hệt nhau được treo vào hai điểm ở cùng độ cao, cách nhau 6 cm. Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng với phương trình lần lượt $x_1 = 6cos \omega t (cm) và x_2 = 12cos(\omega t + π/3) (cm)$. Trong quá trình dao động, khoảng cách lớn nhất giữa hai vật nhỏ của các con lắc bằng

Hai con lắc lò xo giống hệt nhau được treo vào hai điểm ở cùng độ cao, vị trí treo cách nhau một đoạn $8\mathrm{c}\mathrm{m}$ như hình (a). Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng thì đồ thị biến thiên của li độ theo thời gian của hai vật nhỏ được biểu diễn như hình (b). Kể từ thời điểm $\mathrm{t}=0$, thời điểm hai vật nhỏ cách nhau $8\sqrt{2}\mathrm{c}\mathrm{m}$ lần thứ 2024 là

Treo thẳng đứng một con lắc đơn và một con lắc lò xo vào trần một thang máy đang đứng yên tại nơi có gia tốc trọng trường bằng $10\mathrm{m}/{\mathrm{s}}^2$. Kích thích cho hai con lắc dao động điều hòa thì thấy chúng đều có tần số góc bằng $10\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$ và biên độ dài bằng $1\mathrm{c}\mathrm{m}$. Đúng lúc vật nặng của hai con lắc đi qua VCTB thì thang máy bắt đầu chuyển động nhanh dần đều xuống phía dưới với gia tốc $\mathrm{2,5}\mathrm{m}/{\mathrm{s}}^2$. Tỉ số giữa biên độ dài của con lắc đơn và con lắc lò xo sau khi thang máy chuyển động gần nhất với giá trị nào sau đây?