Cho hàm số y = \left| 2 x^{3} - 3 \left(\right. 2 m + 2 \right) x^{2} + 6 \left( m^{2} + m \right) x - m \left|. Có bao nhiêu giá trị nguyên của tham số m \in \left(\right. - 20 \textrm{ } ; \textrm{ } 20 \right) để hàm số đã cho đồng biến trên khoảng $\left( 0 \textrm{ } ; \textrm{ } 1 \right)$?

A.  

$19$.

B.  

$18$.

C.  

$20$.

D.  

$21$.

Đáp án đúng là: C

Cho hàm số $y = \left| 2 x^{3} - 3 \left(\right. 2 m + 2 \right) x^{2} + 6 \left( m^{2} + m \right) x - m \left|$. Có bao nhiêu giá trị nguyên của tham số $m \in \left(\right. - 20 \textrm{ } ; \textrm{ } 20 \right)$ để hàm số đã cho đồng biến trên khoảng $\left( 0 \textrm{ } ; \textrm{ } 1 \right)$?
A. $19$. B. $18$. C. $20$. D. $21$.
Lời giải
Xét hàm số $f \left( x \right) = 2 x^{3} - 3 \left( 2 m + 2 \right) x^{2} + 6 \left( m^{2} + m \right) x - m$
$\Rightarrow f^{'} \left( x \right) = 6 \left[\right. x^{2} - \left( 2 m + 2 \right) x + m^{2} + m \left]\right.$, $\left(\Delta\right)^{'} = m + 1$
Trường hợp 1: $m + 1 \leq 0 \Leftrightarrow m \leq - 1$ suy ra $f^{'} \left( x \right) \geq 0 \textrm{ }\textrm{ } \forall x \in \mathbb{R}$
Vậy để hàm số $y = \left|\right. f \left( x \right) \left|\right.$ đồng biến trên khoảng $\left( 0 ; 1 \right)$ khi và chỉ khi $\left{\right. m \leq - 1 \\ f \left( 0 \right) \geq 0 \Leftrightarrow \left{ m \leq - 1 \\ - m \geq 0 \Leftrightarrow m \leq - 1$
Kết hợp với điều kiện $m \in \mathbb{Z}\&\text{nbsp}; ;   m \in \left(\right. - 20  ;  20 \right)$ ta được $m \in \left{ - 19 ;   - 18 ;   - 17 ;   ⋯ ;   - 3 ;   - 2 ;   - 1 \right}$.
Ta có $19$ giá trị của $m$ thoả mãn yêu cầu bài toán (1)
Trường hợp 2: $m + 1 > 0 \Leftrightarrow m > - 1$ khi đó $f^{'} \left( x \right) = 0 \Leftrightarrow \left[\right. x = m + 1 - \sqrt{m + 1} \\ x = m + 1 + \sqrt{m + 1}$
Bảng xét dấu $f^{'} \left( x \right)$

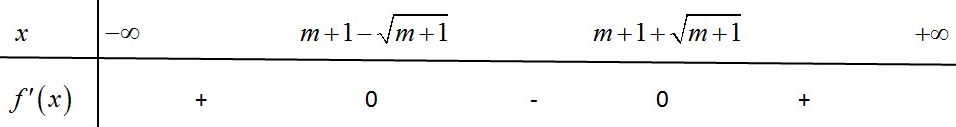
Vậy để hàm số $y = \left|\right. f \left( x \right) \left|\right.$ đồng biến trên khoảng $\left( 0 ; 1 \right)$ khi đó ta có các trường hợp sau
TH 2.1 $\left{\right. m + 1 - \sqrt{m + 1} \geq 1 \\ f \left( 0 \right) \geq 0 \Leftrightarrow \left{\right. m \geq \sqrt{m + 1} \\ m \leq 0 \textrm{ }\textrm{ }\textrm{ }\textrm{ }\textrm{ } V N$
TH2.2 $\left{\right. m + 1 - \sqrt{m + 1} \leq 0 \\ m + 1 + \sqrt{m + 1} \geq 1 \\ f \left( 0 \right) \leq 0 \Leftrightarrow \left{\right. \sqrt{m + 1} - 1 \leq 0 \\ \sqrt{m + 1} \geq - m \\ - m \leq 0 \Leftrightarrow m = 0$
TH2.3 $\left{\right. m + 1 + \sqrt{m + 1} \leq 0 \\ f \left( 0 \right) \geq 0 \Leftrightarrow \left{ \sqrt{m + 1} + 1 \leq 0 \\ - m \geq 0 V N$
Kết hợp với điều kiện ta được: $m = 0$. Do $m \in \mathbb{Z}\&\text{nbsp}; ;   m \in \left(\right. - 20  ;  20 \right)$ Ta có $1$ giá trị của $m$ thoả mãn yêu cầu bài toán $\left( 2 \right) .$
Từ (1) và (2) suy ra: có tất cả có $20$giá trị của $m$ thoả mãn yêu cầu bài toán.