Trang chủ   Hỏi & đáp   THPT Quốc gia   Toán   Câu hỏi số #11398  

Cho hàm số y=x3−6x2+9x+m (C)y = x^{3} - 6 x^{2} + 9 x + m \text{ } \left( C \right), với mm là tham số. Giả sử đồ thị (C)\left( C \right) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn x1<x2<x3x_{1} < x_{2} < x_{3}. Khẳng định nào sau đây đúng?

A.  

1<x1<3<x2<4<x31 < x_{1} < 3 < x_{2} < 4 < x_{3}.

B.  

1<x1<x2<3<x3<41 < x_{1} < x_{2} < 3 < x_{3} < 4.

C.  

0<x1<1<x2<3<x3<40 < x_{1} < 1 < x_{2} < 3 < x_{3} < 4.

D.  

x1<0<1<x2<3<x3<4x_{1} < 0 < 1 < x_{2} < 3 < x_{3} < 4.

Đáp án đúng là: C

Giải thích đáp án:

Cho hàm số y=x3−6x2+9x+m (C)y = x^{3} - 6 x^{2} + 9 x + m \text{ } \left( C \right), với mm là tham số. Giả sử đồ thị (C)\left( C \right) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn x1<x2<x3x_{1} < x_{2} < x_{3}. Khẳng định nào sau đây đúng?
A. 1<x1<3<x2<4<x31 < x_{1} < 3 < x_{2} < 4 < x_{3}. B. 1<x1<x2<3<x3<41 < x_{1} < x_{2} < 3 < x_{3} < 4.
C. 0<x1<1<x2<3<x3<40 < x_{1} < 1 < x_{2} < 3 < x_{3} < 4. D. x1<0<1<x2<3<x3<4x_{1} < 0 < 1 < x_{2} < 3 < x_{3} < 4.
Lời giải
Phương trình hoành độ giao điểm của đồ thị (C) với trục hoành x3−6x2+9x+m=0⇔m=−x3+6x2−9xx^{3} - 6 x^{2} + 9 x + m = 0 \Leftrightarrow m = - x^{3} + 6 x^{2} - 9 x (1). Xét hàm số f(x)=−x3+6x2−9xf \left( x \right) = - x^{3} + 6 x^{2} - 9 x với x∈Rx \in \mathbb{R}.
Ta có f′(x)=−3x2+12x−9=0⇔[x=1x=3f ' \left( x \right) = - 3 x^{2} + 12 x - 9 = 0 \Leftrightarrow \left[\right. x = 1 \\ x = 3.
Ta có f(x)=0⇔−x3+6x2−9x=0⇔[x=0x=3f \left( x \right) = 0 \Leftrightarrow - x^{3} + 6 x^{2} - 9 x = 0 \Leftrightarrow \left[\right. x = 0 \\ x = 3
và f(x)=−4⇔−x3+6x2−9x=−4⇔[x=1x=4f \left( x \right) = - 4 \Leftrightarrow - x^{3} + 6 x^{2} - 9 x = - 4 \Leftrightarrow \left[\right. x = 1 \\ x = 4
BBT của hàm số f(x)f \left( x \right)



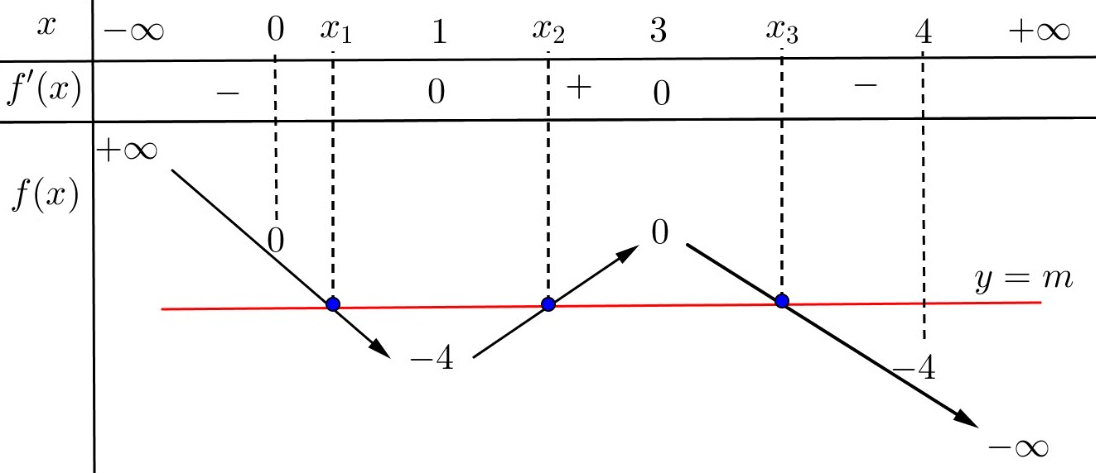
Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt có hoành độ thoả mãn x1<x2<x3x_{1} < x_{2} < x_{3}
⇔\Leftrightarrow Phương trình (1) có 3 nghiệm x1<x2< x3x_{1} < x_{2} < \textrm{ } x_{3}
⇔\Leftrightarrow Đường thẳng y=my = m cắt đồ thị hàm số f(x)f \left( x \right) tại 3 điểm có hoành độ x1<x2<x3x_{1} < x_{2} < x_{3}
Dựa vào BBT ta suy ra 0<x1<1<x2<3<x3<40 < x_{1} < 1 < x_{2} < 3 < x_{3} < 4.
Bản word phát hành từ website Tailieuchuan.vn

Câu hỏi tương tự:

#7544 THPT Quốc giaToán

Cho hàm số f(x)=25x5−m2x4+4(m+3)3x3−(m+7)x2f \left( x \right) = \dfrac{2}{5} x^{5} - \dfrac{m}{2} x^{4} + \dfrac{4 \left( m + 3 \right)}{3} x^{3} - \left( m + 7 \right) x^{2} với mm là tham số. Có bao nhiêu giá trị nguyên của tham số mm để hàm số g(x)=f(∣x∣)g \left( x \right) = f \left( \left|\right. x \left|\right. \right) có đúng một điểm cực đại?

Lượt xem: 128,283 Cập nhật lúc: 23:24 01/08/2024

#8900 THPT Quốc giaToán

Cho hàm số y=x3−3(m+1)x2+9x−my = x^{3} - 3 \left( m + 1 \right) x^{2} + 9 x - m với mm là tham số. Gọi SS là tập hợp các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x1,x2x_{1} , x_{2} sao cho 3x1−2x2=m+63 x_{1} - 2 x_{2} = m + 6. Tích các phần tử của tập SS bằng

Lượt xem: 151,332 Cập nhật lúc: 18:49 02/08/2024

#8701 THPT Quốc giaToán

Cho hàm số

với

là tham số. Có tất cả bao nhiêu giá trị nguyên của

để phương trình

có

nghiệm phân biệt

Lượt xem: 147,933 Cập nhật lúc: 16:34 04/08/2024

#8505 THPT Quốc giaToán

Cho hàm số y=mx−2m−3x−my = \dfrac{m x - 2 m - 3}{x - m} với mm là tham số. Gọi SS là tập hợp tất cả các giá trị nguyên của mm để hàm số đồng biến trên khoảng (2;+∞)\left( 2 ; + \infty \right). Tìm số phần tử của SS

Lượt xem: 144,627 Cập nhật lúc: 11:43 04/08/2024

#8535 THPT Quốc giaToán

Xét hàm số f(t)=9t9t+m2f \left( t \right) = \dfrac{9^{t}}{9^{t} + m^{2}} với mm là tham số thực. Gọi SS là tập hợp tất cả các giá trị của mm sao cho Tìm tổng các phần tử của tập SS.

Lượt xem: 145,131 Cập nhật lúc: 23:36 31/07/2024

#7885 THPT Quốc giaToán

Gọi SS là tập hợp tất cả các giá trị nguyên của tham số sao cho hàm số

xác định với mọi x∈(1;+∞).x \in \left( 1 ; + \infty \right) .Tổng tất cả các phần tử của tập SS bằng

Lượt xem: 134,081 Cập nhật lúc: 18:53 02/08/2024

#7883 THPT Quốc giaToán

Cho hàm số f(x)=1+lnxxf \left( x \right) = \dfrac{1 + ln x}{x} với x>0.x > 0 . Họ nguyên hàm của hàm số f(x)f \left( x \right) là

Lượt xem: 134,042 Cập nhật lúc: 09:54 03/08/2024

#8418 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) xác định với mọi x∈Rx \in \mathbb{R} và có bảng xét dấu của f′(x)f^{'} \left( x \right) như sau:



Số điểm cực trị của hàm số y=f(x)y = f \left( x \right) là:

Lượt xem: 143,137 Cập nhật lúc: 13:53 31/07/2024

#7533 THPT Quốc giaToán

Cho hàm số y=ax+bx+cy = \dfrac{a x + b}{x + c}, có đồ thị là hình vẽ với a,b,ca , b , c là các số nguyên. Tính giá trị của biểu thức T=a−3b+2cT = a - 3 b + 2 c.


Lượt xem: 128,077 Cập nhật lúc: 19:47 31/07/2024


Đề thi chứa câu hỏi này:

Đề Thi Thử TN THPT 2023 Môn Toán - THPT Lý Thái Tổ - Bắc Ninh - Lần 1 (Có Giải Chi Tiết)THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

191 lượt xem 63 lượt làm bài