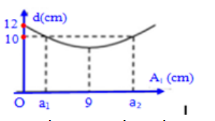
Hai chất điểm cùng khối lượng, dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox, có phương trình lần lượt là x₁=A₁cos(ωt+φ₁) và x₂=A₂cos(ωt+φ₂). Gọi d là khoảng cách lớn nhất giữa hai chất điểm theo phương Ox. Hình bên là đồ thị biểu diễn sự phụ thuộc của d theo A₁ (với A₂,φ₁,φ₂ là các giá trị xác định). Chọn gốc thế năng tại vị trí cân bằng. Nếu W1 là tổng cơ năng của hai chất điểm ở giá trị a₁ và W₂ là tổng cơ năng của hai chất điểm ở giá trị a₂ thì tỉ số W₂/W₁ gần nhất với kết quả nào sau đây?

Hai chất điểm $M$ và $N$ cùng khối lượng dao động điều hòa cùng tần số, cùng biên độ $6\mathrm{c}\mathrm{m}$, dọc theo hai đường thẳng gần nhau và cùng song song với trục $\mathrm{O}\mathrm{x}$. Vị trí cân bằng của $\mathrm{M}$ và $\mathrm{N}$ nằm trên một đường thẳng vuông góc với $\mathrm{O}\mathrm{x}$ tại $\mathrm{O}$. Trong quá trình dao động, hình chiếu của $\mathrm{M}$ và $\mathrm{N}$ lên trục $\mathrm{O}\mathrm{x}$ có khoảng cách lớn nhất là $6\mathrm{c}\mathrm{m}$. Độ lệch pha của hai dao động có độ lớn bằng

Hai chất điểm cùng khối lượng, dao động điều hòa dọc theo trục tọa độ $Ox$ trên hai đường thẳng song song kề nhau, có phương trình lần lượt là $x_1=A_1\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t+{\phi }_1\right)$ và $x_2=A_2\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t+{\phi }_2\right)$. Gọi $d$ là khoảng cách lớn nhất giữa hai chất điểm theo phương $Ox$. Hình bên là đồ thị biểu diễn sự phụ thuộc của $d$ theo $A_1$. Chọn gốc thế năng tại vị trí cân bằng. Nếu $W_1$ là tổng cơ năng của hai chất điểm ở giá trị ${\mathrm{a}}_1$và $W_2$ là tổng cơ năng của hai chất điểm ở giá trị ${\mathrm{a}}_2$ thì tỉ số $W_2/W_1$ gần nhất với giá trị nào sau đây?

Hai chất điểm có cùng khối lượng, dao động điều hòa trên hai đường thẳng song song, có vị trí cân bằng cùng thuộc một đường thẳng vuông góc với các quỹ đạo. Đồ thị biểu diễn sự phụ thuộc của li độ $x_1$ và $x_2$ của hai chất điểm theo thời gian t như hình bên. Kể từ t=0, thời điểm hai chất điểm có cùng li độ lần thứ 2024 thì tỉ số động năng của hai chất điểm $\frac{W_{\mathrm{d}2}}{W_{\mathrm{d}1}}$ là

Một chất điểm có khối lượng 200 g thực hiện đồng thời hai dao động điều hòa cùng tần số, cùng biên độ có li độ phụ thuộc thời gian được biểu diễn như hình vẽ. Biết $t_2-t_1=\frac{1}{3}s$. Lấy ${\pi }^2=10$. Cơ năng của chất điểm có giá trị bằng

Dao động của một chất điểm có khối lượng $10\mathrm{g}$ là tổng hợp của hai dao động điều hòa cùng phương có phương trình lần lượt là ${\mathrm{x}}_1=10\mathrm{c}\mathrm{o}\mathrm{s}\left(10\mathrm{t}+\frac{\mathrm{\pi }}{4}\right)\left(\mathrm{c}\mathrm{m}\right)$ và ${\mathrm{x}}_2=5\mathrm{c}\mathrm{o}\mathrm{s}\left(10\mathrm{t}-\frac{3\mathrm{\pi }}{4}\right)\left(\mathrm{c}\mathrm{m}\right)$. Chọn mốc thế năng ở VTCB. Lấy ${\mathrm{\pi }}^2=10$. Cơ năng của chất điểm bằng:

Một chất điểm có khối lượng m = 300 g thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ. Li độ của hai dao động thành phần phụ thuộc thời gian như hình vẽ. Nếu $t_{2} - t_{1} = \dfrac{1}{6} s$ thì cơ năng của chất điểm gần giá trị nào nhất sau đây?

Một chất điểm có khối lượng $m=100\mathrm{g}$ thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có phương trình lần lượt là $x_1=6\mathrm{c}\mathrm{o}\mathrm{s}\left(10t+\frac{2\pi }{3}\right)(\mathrm{c}\mathrm{m}/\mathrm{s})$ và $x_2=8\mathrm{s}\mathrm{i}\mathrm{n}\left(10t+\frac{2\pi }{3}\right)(\mathrm{c}\mathrm{m}/\mathrm{s})$. Năng lượng dao động của chất điểm này là

Một chất điểm khối lượng $\mathrm{m}=200\mathrm{g}$ đồng thời thực hiện hai dao động điều hòa cùng phương cùng tần số. Ở thời điểm $t$ bất kỳ li độ của hai dao động thành phần này luôn thỏa mãn $16x_1^2+9x_2^2=36\mathrm{}\left({\mathrm{x}}_1\right.$ và ${\mathrm{x}}_2$ tính bằng $\mathrm{c}\mathrm{m}$). Biết lực phục hồi cực đại tác dụng lên chất điểm trong quá trình dao động là $\mathrm{F}=2\mathrm{N}$. Tần số góc của dao động là

Hai chất điểm dao động điều hòa cùng biên độ. Tại $t=0$, chất điểm $M$ (có li độ $x_1$) xuất phát tại vị trí có li độ $5\mathrm{c}\mathrm{m}$ và chất điểm $N$ (có li độ $x_2$) xuất phát tại vị trí cân bằng. Đồ thị sự phụ thuộc của li độ vào thời gian của hai chất điểm như hình. Tốc độ cực đại của chất điểm $M$ gần nhất với giá trị nào sau đây?