
Trắc nghiệm Toán 12: Mặt nón, mặt trụ và mặt cầu
<p>Tổng hợp các bài tập trắc nghiệm chuyên đề Mặt nón, Mặt trụ và Mặt cầu được trích lọc từ các đề thi đại học – THPT Quốc gia những năm gần đây. Nội dung bài tập bao phủ toàn bộ kiến thức trọng tâm: nhận dạng hình, công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của từng loại mặt tròn xoay. Nhiều câu hỏi ở mức vận dụng và vận dụng cao giúp học sinh rèn luyện tư duy không gian, phản xạ tính toán nhanh và chính xác. Tài liệu có đáp án và giải thích chi tiết, phù hợp để luyện thi nước rút, ôn tập hệ thống và làm quen với cấu trúc đề thi thật.</p>
Từ khoá: toán 12 mặt nón mặt trụ mặt cầu bài tập hình khối lớp 12 trắc nghiệm hình học không gian đề thi đại học môn toán ôn thi THPT Quốc gia toán lớp 12 có lời giải luyện thi đại học hình học hình học không gian nâng cao đề toán khối 12
Số câu hỏi: 79 câuSố mã đề: 3 đềThời gian: 1 giờ
153,959 lượt xem 11,839 lượt làm bài
Xem trước nội dung:
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn . Hai mặt phẳng (P), (Q) qua M tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60°. Độ dài đoạn thẳng AB bằng:
Hình nón có diện tích xung quanh bằng 24π và bán kính đường tròn đáy bằng 3. Đường sinh của hình nón có độ dài bằng:
Cho một hình trụ có chiều cao bằng 2 và bán kính đáy bằng 3. Thể tích khối trụ đã cho bằng:
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là :
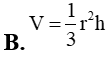
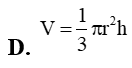
Một khối trụ có thiết diện qua một trục là một hình vuông. Biết diện tích xung quanh của khối trụ bằng . Thể tích V của khối trụ bằng:
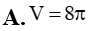
Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng .Khi đó đường cao hình nón bằng:
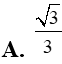
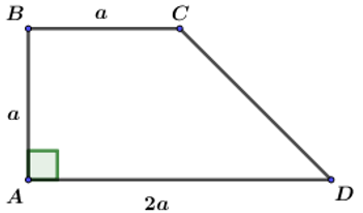
Cho hình thang ABCD có . Tính thể tích khối nón tròn xoay sinh ra khi quay quanh hình thang ABCD xung quanh trục CD?
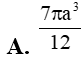
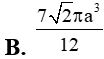
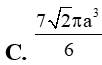
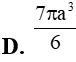
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn . Hai mặt phẳng (P), (Q) qua M và tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng . Độ dài đoạn thẳng AB bằng:
Tính diện tích của mặt cầu có bán kính r=2.
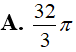
Công thức tính diện tích xung quanh của hình nón có đường sinh l, bán kính đáy r là:
Trong không gian, cho hình chóp S.ABC có SA, AB, BC đôi một vuông góc với nhau và SA=a, SB=b, SC=c. Mặt cầu đi qua S, A, B, C có bán kính bằng;
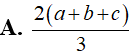
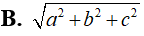
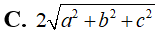
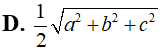
Một hình trụ có bán kính đáy bằng 2cm và có thiết diện qua trục là một hình vuông. Diện tích xung quanh của hình trụ là
Cho tam giác ABC vuông tại A, cạnh AB= 6, AC=8 và M là trung điểm của cạnh AC. Khi đó thể tích của khối tròn xoay do tam giác BMC quanh cạnh AB là:
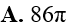
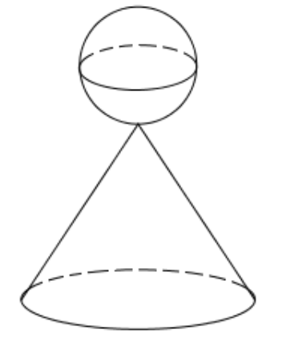
Một khối pha lê gồm một hình cầu bán kính R và một hình nón có bán kính đáy và đường sinh lần lượt là r, l thỏa mãn xếp chồng lên nhau (hình vẽ). Biết tổng diện tích mặt cầu và diện tích toàn phần của hình nón là 91 . Tính diện tích của khối cầu .
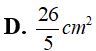
Khối trụ tròn xoay có đường kính là 2a, chiều cao là h=2a có thể tích là:
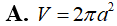
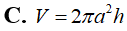
Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh của hình nón là:
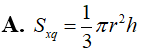
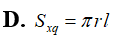
Một khối gỗ hình lập phương có thể tích . Một người thợ mộc muốn gọt giũa khối gỗ đó thành một khối trụ có thể tích là . Tính tỉ số lớn nhất ?
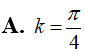
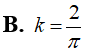
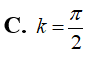
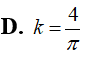
Thể tích của khối nón có chiều cao h = 6 và bán kính đáy R = 4 bằng
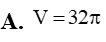
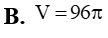
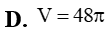
Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Thể tích khối trụ là:
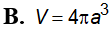
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng ABC và AB = 2, AC = 4, . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là
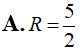
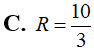
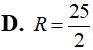
Cho khối nón có bán kính đáy và chiều cao h = 4. Tính thể tích V của khối nón đã cho
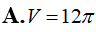
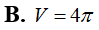
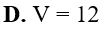
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC; . Điểm I thỏa mãn . M là trung điểm SD, H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , SC Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).
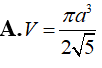
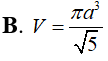
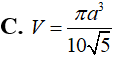
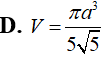
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là 12cm. Giá trị lớn nhất của thể tích khối trụ là:
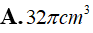
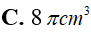
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng a. Tính diện tích xung quanh S của khối trụ đó.
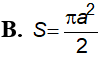
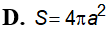
Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu?
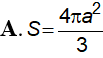
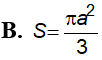
Đề thi tương tự
5 mã đề 139 câu hỏi 1 giờ
185,391 xem14,247 thi
1 mã đề 109 câu hỏi 1 giờ
185,763 xem14,280 thi
2 mã đề 95 câu hỏi 1 giờ
176,613 xem13,580 thi
1 mã đề 14 câu hỏi 1 giờ
160,963 xem12,373 thi
1 mã đề 39 câu hỏi 1 giờ
160,353 xem12,330 thi
1 mã đề 20 câu hỏi 1 giờ
175,013 xem13,456 thi
7 mã đề 175 câu hỏi 1 giờ
179,821 xem13,827 thi
10 mã đề 238 câu hỏi 1 giờ
148,244 xem11,397 thi
4 mã đề 80 câu hỏi 45 phút
154,518 xem11,880 thi
