Tổng hợp đề thi thử THPT môn Toán (Có đáp án và giải thích)

Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A(1;-3;4), B(-2;-5;-7) và C(6;-3;-1). Phương trình đường trung tuyến AM của tam giác ABC là:

Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SA=a tam giác ABC là tam giác vuông cân tại A, AB=2a. Tính theo a thể tích V của khối chóp S.ABC.

Cho hàm số y=f(x) xác định và liên tục trên R có bảng biến thiên sau

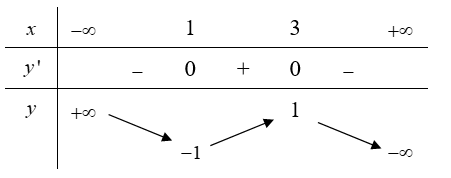
Khẳng định nào sau đây là đúng?

Cho hai số phức $z_1=2+3i, z_2=-4-5i$. Số phức $z=z_1+z_2$ là:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có tâm I(-1;2;0) và bán kính R=3. Phương trình mặt cầu (S) là:

Giới hạn $\underset{x\to -\infty }{Lim}\frac{4x+1}{-x+1}$ bằng bao nhiêu?

Với các số thực a, b bất kì, mệnh đề nào sau đây đúng?

Một tổ gồm 5 học sinh nam và 3 học sinh nữ. Tính số cách chọn cùng lúc 3 học sinh trong tổ đi tham gia chương trình thiện nguyện.

Nguyên hàm của hàm số $f\left(x\right)={\tan }^{2}x$ là

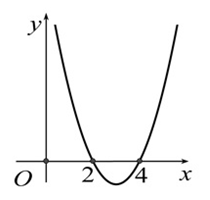
Trục đối xứng của parabol $y=-x^2+5x+3$ là đường thẳng có phương trình là:

Trong mặt phẳng tọa độ Oxy, cho $9x^2+25y^2=225$. Hỏi diện tích hình chữ nhật cơ sở ngoại tiếp (E) là

Cho khối trụ có bán kính hình tròn đáy bằng r và chiều cao bằng h. Hỏi nếu tăng chiều cao lên 2 lần và tăng bán kính đáy lên 3 lần thì thể tích của khối trụ mới sẽ tăng lên bao nhiêu lần?

Số nghiệm của phương trình $|3x-2|=2x-1$ là:

Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên:

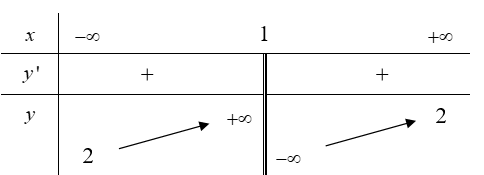
Khẳng định nào dưới đây là đúng?

Đạo hàm của hàm số $y=\frac{x+1}{2^x}$ là

Xem giữa số 3 và số 768 là 7 số để được một cấp số nhân có $u_1=3$. Khi đó $u_5$ bằng:

Gọi $z_1,z_2,z_3,z_4$ là các nghiệm phức của phương trình ( $z^2$ - 4 z )^2 -3 $(z^2-4z)$-40=0. Khi đó, giá trị $H=|z_1{|}^2+|z_2{|}^2+|z_3{|}^2+|z_4{|}^2$ bằng

Trong không gian cho tam giác ABC vuông tại A có AB=a và $\widehat{ACB}=30°$. Thể tích khối nón sinh ra khi quay tam giác ABC quanh trục AC là:

Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) song song với hai đường thẳng $d_1: \frac{x-2}{2}=\frac{y+1}{-3}=\frac{z}{4}$, $d_2:\begin{array}{l}x=2+t\\ y=3+2t\\ z=1-t\end{array}$. Vecto nào sau đây là vecto pháp tuyến của mặt phẳng (P) ?

Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, SA=2a. Thể tích khối chóp S.ABCD theo a là:

Biết hàm số y=f(x) có đồ thị đối xứng với đồ thị hàm số $y=3^x$ qua đường thẳng x=-1. Chọn khẳng định đúng trong các khẳng định sau?

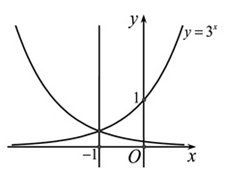
Nguyên hàm F(x) của hàm số $f\left(x\right)=\sin 2x.e^{{\sin }^{2}x}$ là:

Một đề thi môn Toán có 50 câu hỏi trắc nghiệm khách quan, mỗi câu có 4 phương án trả lời, trong đó có đúng một phương án là đáp án. Học sinh chọn đúng đáp án được 0,2 điểm, chọn sai đáp án không được điểm. Một học sinh làm đề thi đó, chọn ngẫu nhiên các phương án trả lời của tất cả 50 câu hỏi, xác suất để học sinh đó được 5,0 điểm bằng:

Cho cấp số cộng (Un) có $u_5=-15, u_{20}=60$. Tổng của 10 số hạng đầu tiên của cấp số cộng này là

Cho hàm số $y=-x^3+3x^2+(2m-1)x+2m-3$ có đồ thị (Cm). Với giá trị nào của tham số m thì tiếp tuyến của hệ số góc lớn nhất của đồ thị (Cm) vuông góc với đường thẳng $△: x-2y-4=0$?

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng: $△: \frac{x}{1}=\frac{y-1}{1}=\frac{z-2}{-1}$ và mặt phẳng (P): x+2y+2z-4=0. Phương trình đường thẳng d nằm trong mặt phẳng (P) sao cho d cắt và vuông góc với đường thẳng Δ là

Họ nguyên hàm của hàm số $f\left(x\right)=\frac{x^5}{x^2+1}$ là:

Cho hàm số y=f(x) liên tục trên R, có đạo hàm $f\text{'}\left(x\right)=(x-1)(x^2-2)(x^4-4)$. Mệnh đề nào sau đây là đúng?

Cho phương trình $9^x+(x-12).3^x+11-x=0$. Phương trình trên có hai nghiệm x1,x2. Giá trị S=x1+x2 bằng bao nhiêu?

Cho hàm số y=f(x) có bảng biến thiên sau

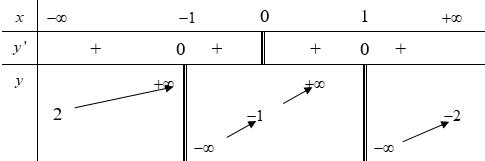
Tất cả các giá trị thực của tham số m để đường thẳng y=1-m cắt đồ thị hàm số đã cho tại hai điểm phân biệt là:

Số nghiệm chung của hai phương trình $4{\cos }^{2}x-3=0$ và $2\sin x+1=0$ trên khoảng $(\frac{-\mathrm{\pi }}{2};\frac{3\mathrm{\pi }}{2})$ bằng

Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và tma giác ABD đều. SO vuông góc mặt phẳng (ABCD) và SO=2a. M là trung điểm của SD. Tang góc giữa CM và (ABCD) là:

Biết n là số nguyên dương thỏa mãn $C_n^{n-1}+C_n^{n-2}=78$, số hạng chứa $x^8$ trong khai triển ${(x3-\frac{2}{x})}^n$ là:

Cho số phức z=a+bi ( $a,b\in R$) thỏa mãn $z+1+2i-(1+i)\left|z\right|=0$ và |z|>1. Tính giá trị của biểu thức P=a+b

Tìm tất cả các giá trị của tham số m để phương trình ${\log }_2\frac{4^x-1}{4^x+1}=m$ có nghiệm thực.

Cho hàm số y=f(x). Hàm số y=f'(x)  có đồ thị như hình bên. Hàm số $y=f(1+x^2)$ nghịch biến trên khoảng nào dưới đây?

Cho hình chóp S.ABCD có đáy là hình vuông cạnh $2\sqrt{2}$, cạnh bên SA vuông góc với mặt phẳng đáy. Mặt phẳng $\left(\alpha \right)$ qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP là

Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, $\widehat{ABC}=60°$, SA vuông góc với (ABCD) $SA=\frac{3a}{2}$. Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng:

Một ô tô đang chuyển động đều với vận tốc 12(m/s) thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc v(t)= -2t+12 (m/s)  (trong đó t là thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe dừng hẳn) thì ô tô đi được quãng đường bao nhiêu?

Trong không gian với hệ tọa độ Oxy, cho đường thẳng $△: \frac{x-1}{2}=\frac{y}{1}=\frac{z+2}{-1}$ và hai điểm A(0;-1;3), B(1;-2;1). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho $M{A}^2+2M{B}^2$ đạt giá trị nhỏ nhất

Cho khối lăng trụ ABC A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C. Cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC A'B'C' là

Cho đồ thị hàm số $\left(C\right): y=x^4-(3m+1)x^2+m^2$ (m là tham số). Để (C) cắt trục hoành tại bốn phân biệt có hoành độ lập thành cấp số cộng thì giá trị của m là:

Cho hàm số f(x) có đạo hàm liên tục trên [0;3] thỏa mãn f(3)=0,  và ${\int }_0^3{[f\text{'}(x\left)\right]}^{2}dx=\frac{7}{6}$ và ${\int }_0^3\frac{f\left(x\right)}{\sqrt{x+1}}dx=-\frac{7}{3}$. Tích phân ${\int }_0^{3}f\left(x\right)dx$ bằng:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2;1;1) và mặt phẳng $\left(\alpha \right): x+y+z-4=0$ và mặt cầu $\left(S\right): x^2+y^2+z^2-6x-6y-8z+18=0$. Phương trình đường thẳng d đi qua M và nằm trong mặt phẳng $\left(\alpha \right)$ cắt mặt cầu (S) theo một đoạn thẳng có độ dài nhỏ nhất là

Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C thành một hàng ngang. Xác suất để trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau bằng:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.

Cho lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi S là điểm đối xứng của A qua BC'. Thể tích khối đa diện ABCSB'C' là

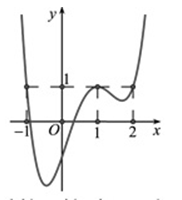
Cho hàm số y=f(x) có đạo hàm trên R. Hàm số y=f'(x) có đồ thị như hình vẽ bên. Đặt y=g(x)=f(x)-x. Khẳng định nào sau đây là đúng?

Cho phương trình $5^x+m={\log }_5(x-m)$ với m là tham số. Có bao nhiêu giá trị nguyên của $m\in (-20;20)$  để phương trình đã cho có nghiệm?

Cho số phức z=1+i. Biết rằng tồn tại các số phức $z_1=a+5i, z_2=b$ (trong đó $a,b\in R, b>1$) thỏa mãn $\sqrt{3}|z-z_1|=\sqrt{3}|z-z_2|=|z_1-z_2|$. Tính b-a.