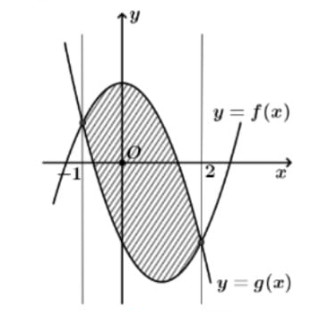
Gọi $\left( D \right)$ là diện tích hình phẳng giới hạn bởi hai đường cong $y = f \left( x \right) = a x^{2} + b x + c$ và $y = g \left( x \right) = - x^{2} + m x + n$. Biết $S_{\left( D \right)} = 9$ và đồ thị hàm số $y = g \left( x \right)$ có đỉnh $I \left( 0 ; 2 \right)$. Khi cho miền được giới hạn bởi hai đường cong trên và hai đường thẳng $x = - 1 ; x = 2$ quay quanh trục $O x$, ta nhận được vật thể tròn xoay có thể tích $V$. Giá trị của $V$ bằng:

Gọi $\left( D \right)$ là diện tích hình phẳng được giới hạn bởi hai đường cong $y = f \left( x \right) = a x^{2} + b x + c$ và $y = g \left( x \right) = - x^{2} + m x + n$. Biết $S_{\left( D \right)} = 9$ và đồ thị hàm số $y = g \left( x \right)$ có đỉnh $I \left( 0 ; 2 \right)$. Khi cho miền được giới hạn bởi hai đường cong trên và hai đường thẳng $x = - 1 ; \textrm{ } x = 2$ quay quanh trục $O x$, ta nhận được vật thể tròn xoay có thể tích $V$. Giá trị của $V$ bằng:

Gọi S là diện tích hình phẳng giới hạn bởi các đường $y = f \left( x \right)$, trục hoành và hai đường thẳng $x = - 3 , x = 2$(như hình vẽ). Đặt $a = \int_{- 3}^{1} f \left( x \right) d x , b = \int_{1}^{2} f \left( x \right) d x$

Gọi diện tích hình phẳng giới hạn bởi đồ thị hàm số $\left( C \right) : y = \dfrac{- 3 x - 1}{x - 1}$ và hai trục tọa độ là $S$. Tính $S ?$

Biết $F \left( x \right)$ và $G \left( x \right)$ là hai nguyên hàm của hàm số $f \left( x \right)$ trên $\mathbb{R}$ và $\int_{0}^{4} f \left( x \right) = F \left( 4 \right) - G \left( 0 \right) + 2 m \left( m > 0 \right)$. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y = F \left( x \right) , y = G \left( x \right) , x = 0$ và $x = 4$. Khi $S = 8$ thì $m$ bằng:

Biết $F \left( x \right)$ và $G \left( x \right)$ là hai nguyên hàm của hàm số $f \left( x \right)$ trên $\mathbb{R}$ và thoả mãn $\int_{0}^{4} f \left( x \right) \text{d} x = F \left( 4 \right) - G \left( 0 \right) + 2 m$, với $m > 0$. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y = F \left( x \right)$, $y = G \left( x \right)$; $x = 0$ và $x = 4$. Khi $S = 8$ thì $m$ bằng

Cho hàm số $y = f \left( x \right)$ liên tục trên $\mathbb{R}$ có đồ thị như hình vẽ dưới. Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f \left( x \right)$, trục hoành và các đường thẳng $x = - 1 , \textrm{ } x = 5 .$

Gọi S là diện tích hình phẳng giới hạn bởi các đường $y = 5^{x} , x = 2$, trục hoành và trục tung. Mệnh đề nào sau đây là đúng?

Cho hàm số $f \left( x \right)$ liên tục trên $\mathbb{R}$. Gọi S là diện tích hình phẳng giới hạn bởi các đường $y = f \left( x \right) , y = 0 , x = - 1 , x = 2$ (như hình vẽ bên). Mệnh đề nào dưới đây đúng?

Gọi $\left( H \right)$ là hình phẳng giới hạn bởi các đường $y = sin x , O x , x = 0 , x = \pi$. Diện tích của hình phẳng $\left( H \right)$ bằng