Có bao nhiêu giá trị nguyên dương không vượt quá 2024 của $y$ thỏa mãn \dfrac{ln3 x}{4 x + 1} \leq ln \left(\right. \dfrac{2 x y}{4 x + 1} \right) đúng với mọi số thực dương $x$?

A.  

2023.

B.  

2021.

C.  

2024.

D.  

2022.

Đáp án đúng là: B

Ta có $\dfrac{ln3 x}{4 x + 1} \leq ln \left( \dfrac{2 x y}{4 x + 1} \right) \Leftrightarrow \dfrac{ln3 x}{4 x + 1} \leq ln \left( \dfrac{2 x}{4 x + 1} \right) + ln y \Leftrightarrow \dfrac{ln3 x}{4 x + 1} - ln \left( \dfrac{2 x}{4 x + 1} \right) \leq ln y$.
Xét hàm số $f \left( x \right) = \dfrac{ln3 x}{4 x + 1} - ln \left( \dfrac{2 x}{4 x + 1} \right)$.
Ta có: $f^{'} \left( x \right) = \dfrac{1}{x \left( 4 x + 1 \right)} - \dfrac{4ln3 x}{\left( 4 x + 1 \right)^{2}} - \left( \dfrac{2 x}{4 x + 1} \right)^{'} . \dfrac{4 x + 1}{2 x}$
$= \dfrac{1}{x \left( 4 x + 1 \right)} - \dfrac{4ln3 x}{\left( 4 x + 1 \right)^{2}} - \dfrac{1}{x \left( 4 x + 1 \right)} = - \dfrac{4ln3 x}{\left( 4 x + 1 \right)^{2}}$.
Suy ra: $f^{'} \left( x \right) = 0 \Leftrightarrow x = \dfrac{1}{3}$.
Bảng biến thiên của hàm số $y = f \left( x \right)$ như sau

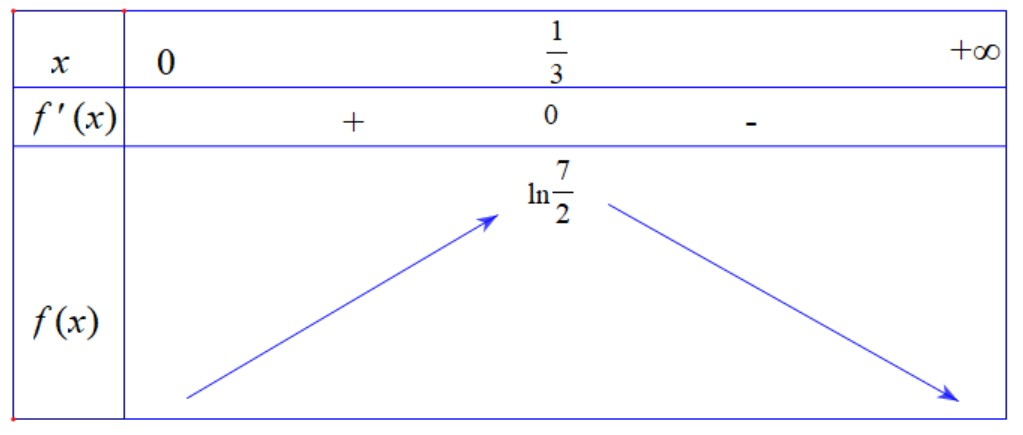
Theo đề ra $\dfrac{ln3 x}{4 x + 1} - ln \left( \dfrac{2 x}{4 x + 1} \right) \leq ln y , \forall x > 0$ nên từ BBT ta phải có $ln y \geq ln \dfrac{7}{2} \Leftrightarrow y \geq \dfrac{7}{2}$
Mặt khác $\left{ y \in \left(\mathbb{Z}\right)^{+} \\ y \leq 2024$ nên $y \in \left{\right. 4 ; 5 ; 6 ; . . . ; 2024 \right}$. Vậy có tất cả 2021 số.