Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7890

Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a3 a. Tính diện tích toàn phần của hình trụ đã cho.

A.  

13πa26\dfrac{13 \pi a^{2}}{6}.

B.  

27πa22\dfrac{27 \pi a^{2}}{2}.

C.  

9πa29 \pi a^{2}.

D.  

9πa22\dfrac{9 \pi a^{2}}{2}.

Đáp án đúng là: B

(TH):
Phương pháp:
Diện tích toàn phần hình trụ Sxq+2Sday=2πrh+2πr2S_{x q} + 2 S_{d a y} = 2 \pi r h + 2 \pi r^{2}
Cách giải:



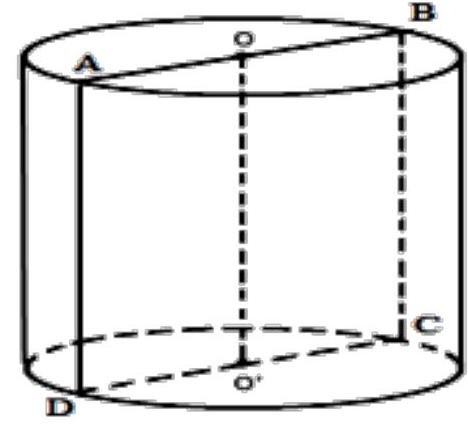
Gọi thiết diện qua trục là hình vuông ABCDA B C D.
Theo đề thì AB=AD=3aA B = A D = 3 a.
Bán kính đáy của hình trụ là R=AB2=3a2R = \dfrac{A B}{2} = \dfrac{3 a}{2}.
Đường sinh của hình trụ là l=AD=3al = A D = 3 a.
Áp dụng công thức diện tích toàn phần của hình trụ, ta có
Stp=2πRl+2πR2=2π.3a2.3a+2π(3a2)2=27πa22S_{t p} = 2 \pi R l + 2 \pi R^{2} = 2 \pi . \dfrac{3 a}{2} . 3 a + 2 \pi \left( \dfrac{3 a}{2} \right)^{2} = \dfrac{27 \pi a^{2}}{2}.


 

Câu hỏi tương tự:

#8840 THPT Quốc giaToán

Cắt một khối trụ bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có cạnh bằng 2a2 a. Thể tích của khối trụ đã cho bằng

Lượt xem: 150,347 Cập nhật lúc: 05:39 17/01/2025

#8508 THPT Quốc giaToán

Cắt hình trụ bởi một mặt phẳng qua trục, ta được thiết diện là một hình vuông có chu vi là 8. Diện tích xung quanh của hình trụ đã cho bằng

Lượt xem: 144,724 Cập nhật lúc: 23:02 18/01/2025

#8635 THPT Quốc giaToán

Cho hình trụ có hai đáy là hình tròn tâm OO và O′O^{'}, chiều cao h=a3h = a \sqrt{3}. Mặt phẳng đi qua tâm OO và tạo với OO′O O^{'} một góc 30∘30 \circ, cắt hai đường tròn tâm OO và O′O^{'} tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng 3a23 a^{2}. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng

Lượt xem: 146,878 Cập nhật lúc: 18:32 18/01/2025

#8572 THPT Quốc giaToán

Cho hình trụ có bán kinh đáy bằng

. Cắt hình trụ bởi một mặt phằng song song với trục, cách trục một khoảng bằng

ta được thiết diện là một hình chữ nhật có chu vi bằng 10a10 a. Thể tích khối trụ đã cho bằng

Lượt xem: 145,808 Cập nhật lúc: 22:57 18/01/2025

#8881 THPT Quốc giaToán

Cho hình trụ có bán kính đáy bằng RR và chiều cao bằng 3R2\dfrac{3 R}{2}. Mặt phẳng (α)\left( \alpha \right) song song với trục của hình trụ và cách trục một khoảng bằng R2\dfrac{R}{2}. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng (α)\left( \alpha \right) là

Lượt xem: 151,070 Cập nhật lúc: 09:42 17/01/2025

#7549 THPT Quốc giaToán

Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng aa. Một mặt phẳng thay đổi, vuông góc với SOS O và cắt SOS O, SAS A, SBS B, SCS C, SDS D lần lượt tại II, MM, NN, PP, QQ. Một hình trụ có một đáy là đường tròn ngoại tiếp tứ giác MNPQM N P Q và một đáy nằm trên mặt phẳng (ABCD)\left( A B C D \right). Thể tích khối trụ lớn nhất bằng

Lượt xem: 128,408 Cập nhật lúc: 19:38 18/01/2025

#8387 THPT Quốc giaToán

Cho hình trụ có hai đáy là hai hình tròn (O;R)\left( O ; R \right) và (O′,R)\left( O^{'} , R \right), chiều cao 2R2 R. Một mặt phẳng (α)\left( \alpha \right) đi qua trung điểm của OO′O O^{'} và tạo với OO′O O^{'} một góc 30∘30 \circ. Mặt phẳng (α)\left( \alpha \right) cắt đường tròn đáy (O;R)\left( O ; R \right) tại hai điểm A, BA , \textrm{ } B. Tính độ dài đoạn thẳng ABA B theo RR?

Lượt xem: 142,621 Cập nhật lúc: 18:35 18/01/2025

#8353 THPT Quốc giaToán

Cho khối trụ có hai đáy lần lượt là hình tròn tâm O,O′O , O^{'} và chiều cao bằng 2a\sqrt{2} a. Một mặt phẳng đi qua tâm OO, tạo với OO′O O^{'} một góc (30)@\left(30\right)^{@} đồng thời cắt hai đường tròn tâm O,O′O , O^{'} tại bốn điểm tạo thành bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng 2a22 a^{2}. Thể tích của khối trụ đã cho bằng

Lượt xem: 142,043 Cập nhật lúc: 18:18 18/01/2025

#8469 THPT Quốc giaToán

Bạn An định làm một cái hộp quà lưu niệm (không nắp) bằng cách cắt từ một tấm bìa hình tròn bán kính 4 cm4 \textrm{ } \text{cm} để tạo thành một khối lăng trụ lục giác đều, biết 6 hình chữ nhật có các kích thước là 1  cm1 \textrm{ }\textrm{ } \text{cm} và x  cmx \textrm{ }\textrm{ } \text{cm} (tham khảo hình vẽ). Thể tích của hộp quà gần nhất với giá trị nào sau đây?

Lượt xem: 144,054 Cập nhật lúc: 18:25 18/01/2025


Đề thi chứa câu hỏi này:

17. Đề thi thử TN THPT môn Toán năm 2024 - THPT Ba Đình - Thanh Hóa - Lần 1.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

5,039 lượt xem 2,667 lượt làm bài