Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7806

Cho hình chóp S.ABCS . A B C với SA=2S A = 2; BC=2B C = 2. Một hình cầu bán kính 4 tiếp xúc với mặt phẳng (ABC)\left( A B C \right) tại CC, tiếp xúc với SAS A tại SS và cắt SBS B tại điểm thứ hai DD sao cho CDC D đi qua tâm của mặt cầu. Tính thể tích của khối chóp S.ABCS . A B C.

A.  

1617\dfrac{16}{17}.

B.  

83\dfrac{8}{3}.

C.  

8351\dfrac{8 \sqrt{3}}{51}.

D.  

312\dfrac{\sqrt{3}}{12}.

Đáp án đúng là: C



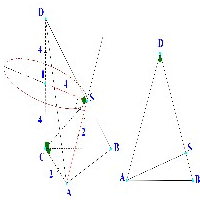
Gọi II là tâm mặt cầu theo đề bài. Theo giả thiết ta có IS⊥SAI S \bot S A(1)
Đồng thời I∈CDI \in C D và DC⊥(BCA)D C \bot \left( B C A \right) tại CC ⇒\Rightarrow IC⊥ACI C \bot A C(2)
Từ (1),(2)\left( 1 \right) , \left( 2 \right) ta suy ra AC=SA=2=BCA C = S A = 2 = B C (do ΔIAC=ΔISA\Delta I A C = \Delta I S A)
Đồng thời DB=DA=DC2+CA2=217D B = D A = \sqrt{D C^{2} + C A^{2}} = 2 \sqrt{17} (do ΔACD=ΔBCD\Delta A C D = \Delta B C D).
Xét cát tuyến BSDB S D và tiếp tuyến BCB Cđối với mặt cầu (I;CD2)\left( I ; \dfrac{C D}{2} \right).
Suy ra BC2=BS.BD⇒BS=21717⇒BSBD=117B C^{2} = B S . B D \Rightarrow B S = \dfrac{2 \sqrt{17}}{17} \Rightarrow \dfrac{B S}{B D} = \dfrac{1}{17} ⇒VB.SACVB.ACD=117\Rightarrow \dfrac{V_{B . S A C}}{V_{B . A C D}} = \dfrac{1}{17}(3)
Xét tam giác ΔDSA\Delta D S A và ΔDAB\Delta D A B có
cosDAB^=cosSDA^⇔DA2+DS2−SA22.DA.DS=DA2+DB2−AB22.DA.DBcos \widehat{D A B} = cos \widehat{S D A} \Leftrightarrow \dfrac{D A^{2} + D S^{2} - S A^{2}}{2 . D A . D S} = \dfrac{D A^{2} + D B^{2} - A B^{2}}{2 . D A . D B} ⇒AB2=4⇒AB=2\Rightarrow A B^{2} = 4 \Rightarrow A B = 2
Suy ra ΔABC\Delta A B C đều có cạnh AB=BC=CA=2A B = B C = C A = 2.
Do đó, từ (3)\left( 3 \right), ta có: VS.ABC=117VD.ABC=117.13.DC.AB234=8351V_{S . A B C} = \dfrac{1}{17} V_{D . A B C} = \dfrac{1}{17} . \dfrac{1}{3} . D C . \dfrac{A B^{2} \sqrt{3}}{4} = \dfrac{8 \sqrt{3}}{51}.


 

Câu hỏi tương tự:

#11390 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C \text{D} có đáy ABCDA B C \text{D} là hình chữ nhật, AB=3, AD=4A B = 3 , \textrm{ } A \text{D} = 4 và các cạnh bên của hình chóp tạo với mặt đáy một góc 60∘60 \circ. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.

Lượt xem: 193,767 Cập nhật lúc: 22:11 25/04/2025

#7549 THPT Quốc giaToán

Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng aa. Một mặt phẳng thay đổi, vuông góc với SOS O và cắt SOS O, SAS A, SBS B, SCS C, SDS D lần lượt tại II, MM, NN, PP, QQ. Một hình trụ có một đáy là đường tròn ngoại tiếp tứ giác MNPQM N P Q và một đáy nằm trên mặt phẳng (ABCD)\left( A B C D \right). Thể tích khối trụ lớn nhất bằng

Lượt xem: 128,469 Cập nhật lúc: 19:34 25/04/2025

#7785 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình thang CBA^=BAD^=90∘\widehat{C B A} = \widehat{B A D} = 90 \circ, AB=BC=2aA B = B C = 2 a, AD=aA D = a. Biết rằng SA=SBS A = S B và SCD^=90∘\widehat{S C D} = 90 \circ. Cạnh bên SAS A hợp với đáy một góc 45∘45 \circ. Gọi φ\varphi là góc giữa hai mặt phẳng (SAB)\left( S A B \right) và (ABCD)\left( A B C D \right). Khẳng định nào dưới đây đúng?

Lượt xem: 132,515 Cập nhật lúc: 22:01 25/04/2025

#7554 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D đáy là hình chữ nhật, AB=2aA B = 2 a, AD=a3A D = a \sqrt{3}. Cạnh bên SAS A vuông góc với đáy. Gọi MM là trung điểm của cạnh CDC D. Biết SMS M tạo với mặt phẳng đáy một góc 60∘60 \circ. Tính thể tích VV của khối chóp S.ABCDS . A B C D.

Lượt xem: 128,546 Cập nhật lúc: 21:58 22/04/2025

#8740 THPT Quốc giaToán

Cho hình trụ có tâm hai đường tròn đáy lần lượt là OOvà O′O ', bán kính đáy hình trụ bằng aa. Trên đường tròn đáy (O)\left( O \right)và (O′)\left( O ' \right)lần lượt lấy hai điểm A,BA , Bsao cho ABA Btạo với trục của hình trụ một góc (30)0\left(30\right)^{0} và có khoảng cách đến trục của hình trụ bằng a32\dfrac{a \sqrt{3}}{2}. Tính thể tíc khối chóp O.O′ABO . O ' A B

Lượt xem: 148,653 Cập nhật lúc: 11:18 23/04/2025

#8288 THPT Quốc giaToán

Cho khối chóp S.ABCDS . A B C Dcó đáy là hình vuông cạnh aa, SAS A vuông góc với mặt phẳng đáy và SCS C tạo với mặt phẳng đáy một góc bằng (60)0\left(60\right)^{0}.Thể tích của khối chóp đã cho bằng

Lượt xem: 140,973 Cập nhật lúc: 16:59 24/04/2025

#7646 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có SAS A vuông góc với (ABC)\left( A B C \right), tam giác ABCA B C đều cạnh bằng a,  SA=a3a , \textrm{ }\textrm{ } S A = a \sqrt{3}. Góc giữa đường thẳng SCS C và mặt phẳng (ABC)\left( A B C \right) bằng


Lượt xem: 130,114 Cập nhật lúc: 13:47 25/04/2025

#7734 THPT Quốc giaToán

Cho hình chóp tam giác S.ABCS . A B C có SAS A vuông góc với mặt phẳng (ABC)\left( A B C \right), SA=aS A = a, tam giác ABCA B C vuông cân tại AA, AB=aA B = a. Thể tích hình chóp S.ABCS . A B C bằng

Lượt xem: 131,555 Cập nhật lúc: 11:13 25/04/2025

#7524 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh a,SA=2aa , S A = 2 a và SAS A vuông góc với đáy. Tính theo aa khoảng cách từ AA đến mặt phẳng (SBD)\left( S B D \right).

Lượt xem: 128,072 Cập nhật lúc: 16:06 25/04/2025


Đề thi chứa câu hỏi này:

51. Đề thi thử TN THPT môn Toán năm 2024 - THPT CHUYÊN HẠ LONG - QUẢNG NINH - LẦN 2

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,636 xem347 thi