Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8449

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình bình hành. Hai điểm M,  NM , \textrm{ }\textrm{ } N lần lượt thuộc các đoạn thẳng ABA B và ADA D (M và N không trùng với A) sao cho 2ABAM+3ADAN=8\dfrac{2 A B}{A M} + \dfrac{3 A D}{A N} = 8. Kí hiệu V,  V1V , \textrm{ }\textrm{ } V_{1} lần lượt là thể tích của các khối chóp S.ABCDS . A B C D và S.MBDN.S . M B D N . Giá trị lớn nhất của tỉ số V1V\dfrac{V_{1}}{V} bằng

A.  

23\dfrac{2}{3}.

B.  

613\dfrac{6}{13}.

C.  

516\dfrac{5}{16}.

D.  

25\dfrac{2}{5}.

Đáp án đúng là: C

(VDC):
Cách giải:



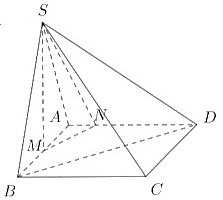
Ta có: VSAMNVSABD=13d(S,(ABCD)).SAMN13d(S,(ABCD)).SABD=SAMNSABD=AM.ANAB.AD\dfrac{V_{S A M N}}{V_{S A B D}} = \dfrac{\dfrac{1}{3} d \left(\right. S , \left( A B C D \right) \left.\right) . S_{A M N}}{\dfrac{1}{3} d \left(\right. S , \left( A B C D \right) \left.\right) . S_{A B D}} = \dfrac{S_{A M N}}{S_{A B D}} = \dfrac{A M . A N}{A B . A D}
Lại có: 2ABAM+3ADAN≥26.ABAM.ADAN⇒8≥26AB.ADAM.AN⇒AB.ADAM.AN≤83\dfrac{2 A B}{A M} + \dfrac{3 A D}{A N} \geq 2 \sqrt{6 . \dfrac{A B}{A M} . \dfrac{A D}{A N}} \Rightarrow 8 \geq 2 \sqrt{6 \dfrac{A B . A D}{A M . A N}} \Rightarrow \dfrac{A B . A D}{A M . A N} \leq \dfrac{8}{3}
Suy ra VSAMN VSABD ≤38⇒VSAMN ≥38VSABD \dfrac{V_{\text{SAMN}\&\text{nbsp};}}{V_{\text{SABD}\&\text{nbsp};}} \leq \dfrac{3}{8} \Rightarrow V_{\text{SAMN}\&\text{nbsp};} \geq \dfrac{3}{8} V_{\text{SABD}\&\text{nbsp};}
Ta có: VSMBND=VSABD−VSAMN≤VSABD−38VSABCD=58VSABCDV_{S M B N D} = V_{S A B D} - V_{S A M N} \leq V_{S A B D} - \dfrac{3}{8} V_{S A B C D} = \dfrac{5}{8} V_{S A B C D}
Suy ra VSMBND≤516VSABCD V_{S M B N D} \leq \dfrac{5}{16} V_{\text{SABCD}\&\text{nbsp};}


 

Câu hỏi tương tự:

#8944 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCD\text{ABCD} là hình bình hành. Gọi MM là trung điểm cạnh AD\text{AD}. Gọi V1,V2V_{1} , V_{2} lần lượt là thể tích của hai khối chóp S.ABMS . A B M và S.ABCS . A B C thì V1V2\dfrac{V_{1}}{V_{2}} bằng

Lượt xem: 152,076 Cập nhật lúc: 05:56 19/11/2024

#8304 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình bình hành, trên cạnh SAS A lấy điểm MM và đặt SMSA=x\dfrac{S M}{S A} = x. Giá trị xx để mặt phẳng (MBC)\left( M B C \right) chia khối chóp đã cho thành hai phần có thể tích bằng nhau là:

Lượt xem: 141,233 Cập nhật lúc: 03:06 21/11/2024

#8566 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình bình hành. Goi MM là trung điem cua cạnh SAS A. Mặt phȁng (α)\left( \alpha \right) đi qua MM và song song với mặt phȁng (SBC)\left( S B C \right) chia khối chóp S.ABCDS . A B C D thành hai phần. Tính tỉ số của thể tích phần chứa đỉnh SS và thể tích phần còn lại.

Lượt xem: 145,650 Cập nhật lúc: 20:52 18/11/2024

#11178 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình bình hành. Mặt bên SADS A D là tam giác đều cạnh a3a \sqrt{3}. ACDA C D là tam giác vuông tại AA có cạnh AC=aA C = a, góc giữa đường thẳng ABA B và mặt phẳng (SAD)\left( S A D \right) bằng (60)0\left(60\right)^{0}. Thể tích khối chóp S.ABCDS . A B C D bằng

Lượt xem: 190,047 Cập nhật lúc: 05:57 19/11/2024

#7866 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình bình hành và SA=SB=SC=aS A = S B = S C = a, hình chiếu vuông góc của SS lên mặt phẳng ABCDA B C D thuộc đoạn ACA C (không trùng với A,CA , C). Giá trị lớn nhất của thể tích khối chóp S.ABCDS . A B C D là:

Lượt xem: 133,788 Cập nhật lúc: 12:02 21/11/2024

#8615 THPT Quốc giaToán

Cho khối chóp S.ABCDS . A B C D có đáy là hình bình hành tâm OO, biết thể tích khối chóp S.OADS . O A D bằng 10cm310 c m^{3}. Thể tích khối chóp S.ABCDS . A B C D bằng?

Lượt xem: 146,520 Cập nhật lúc: 02:59 21/11/2024

#7569 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình chữ nhật, AB=2aA B = 2 a, AD=3aA D = 3 a, mặt bên SABS A B là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SAB)\left( S A B \right) và (SCD)\left( S C D \right) bằng

Lượt xem: 128,704 Cập nhật lúc: 23:57 18/11/2024

#7730 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh bằng 2\sqrt{2}, cạnh bên SAS A vuông góc với mặt đáy và SA=1S A = 1. Khoảng cách giữa hai đường thẳng SBS B và ACA C bằng

Lượt xem: 131,476 Cập nhật lúc: 17:28 20/11/2024

#7785 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình thang CBA^=BAD^=90∘\widehat{C B A} = \widehat{B A D} = 90 \circ, AB=BC=2aA B = B C = 2 a, AD=aA D = a. Biết rằng SA=SBS A = S B và SCD^=90∘\widehat{S C D} = 90 \circ. Cạnh bên SAS A hợp với đáy một góc 45∘45 \circ. Gọi φ\varphi là góc giữa hai mặt phẳng (SAB)\left( S A B \right) và (ABCD)\left( A B C D \right). Khẳng định nào dưới đây đúng?

Lượt xem: 132,412 Cập nhật lúc: 01:43 22/11/2024


Đề thi chứa câu hỏi này:

04. Đề thi thử TN THPT môn Toán năm 2024 - THPT Lý Thái Tổ - Bắc Ninh lần 1.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

5,181 lượt xem 2,758 lượt làm bài